题目内容
17.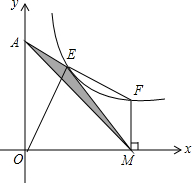 如图,E,F在双曲线y=$\frac{8}{x}$上,FE交y轴于点A,AE=EF,FM⊥x轴于M,求S△AME.
如图,E,F在双曲线y=$\frac{8}{x}$上,FE交y轴于点A,AE=EF,FM⊥x轴于M,求S△AME.
分析 过点E作ED⊥x轴于点D,设点E坐标为(m,$\frac{8}{m}$),点F坐标为(n,$\frac{8}{n}$).由AE=EF可得出OD=DM,即n=2m,由S△AEM=S梯形OMFA-S△AOM-S△EFM结合坐标系中点的意义以及梯形中位线的性质即可得出结论.
解答 解:过点E作ED⊥x轴于点D,如图所示.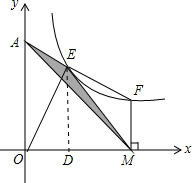
设点E坐标为(m,$\frac{8}{m}$),点F坐标为(n,$\frac{8}{n}$).
∵AE=EF,
∴OD=DM,即m=n-m,
∴n=2m.
S△AEM=S梯形OMFA-S△AOM-S△EFM
=$\frac{1}{2}$(FM+AO)•OM-$\frac{1}{2}$OA•OM-$\frac{1}{2}$FM•DM
=$\frac{1}{2}$×2•$\frac{8}{m}$•n-$\frac{1}{2}$•(2•$\frac{8}{m}$-$\frac{8}{n}$)•n-$\frac{1}{2}$•$\frac{8}{n}$•(n-m)
=16-12-2
=2.
点评 本题考查了坐标系中点的意义、梯形的面积公式、三角形的面积公式以及梯形中位线的性质,解题的关键是找出n=2m.本题属于基础题,难度不大,解决该题型题目时,由给定条件找出E、F点横坐标的关系,再结合梯形中位线的性质以及梯形和三角形的面积公式得出结论.

练习册系列答案
相关题目
9.设a=$\sqrt{2}-1$,b=$\sqrt{5}$-2,c=$\sqrt{10}$-3.则a、b、c的大小关系为( )
| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | c<b<a |
 如图,在?ABCD中,已知E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF.
如图,在?ABCD中,已知E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF.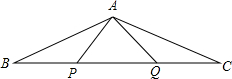 如图,P,Q是△ABC的边BC上的两点,且BP=QC=AP=AQ.
如图,P,Q是△ABC的边BC上的两点,且BP=QC=AP=AQ.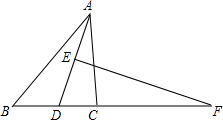 如图,在△ABC中,AD的垂直平分线交AD于E,交BC的延长线于F,FD2=FB•FC,求证:AD平分△BAC.
如图,在△ABC中,AD的垂直平分线交AD于E,交BC的延长线于F,FD2=FB•FC,求证:AD平分△BAC.