题目内容
13.△ABC是等腰三角形,AC为一腰,∠A=30°,CD⊥AB于点D,若AB=6,则高CD的长为3或$\sqrt{3}$.分析 根据题意画出两种情况,①AB=AC,根据含30°角的直角三角形性质求出即可;②AC=BC,求出AD,根据含30°角的直角三角形性质和勾股定理得出AD=$\sqrt{3}$CD,即可求出CD.
解答 解:分为两种情况:①如图1,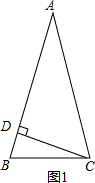
当AB为另一腰时,
∵AB=6,
∴AC=AB=6,
∵CD⊥AB,
∴∠ADC=90°,
∵∠A=30°,
∴CD=$\frac{1}{2}$AC=3;
②如图2,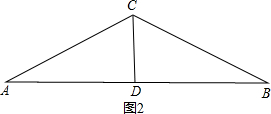
当BC为另一腰时,
∵AB=6,CD⊥AB,
∴∠ADC=90°,AD=BD=3,
∵∠A=30°,
∴AD=$\sqrt{3}$CD,
∴CD=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$;
故答案为:3或$\sqrt{3}$.
点评 本题考查了勾股定理和含30°角直角三角形性质的应用,能熟记含30°角的直角三角形性质是解此题的关键,用了分类讨论思想.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
1. 某路段某时段用雷达测速仪随机监测了200辆汽车的时速,得到如下频数分布表(不完整):注:30-40为时速大于或等于30千米而小于40千米,其它类同.
某路段某时段用雷达测速仪随机监测了200辆汽车的时速,得到如下频数分布表(不完整):注:30-40为时速大于或等于30千米而小于40千米,其它类同.
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果此路段该时间段经过的车有1000辆.估计约有多少辆车的时速大于或等于 60千米.
 某路段某时段用雷达测速仪随机监测了200辆汽车的时速,得到如下频数分布表(不完整):注:30-40为时速大于或等于30千米而小于40千米,其它类同.
某路段某时段用雷达测速仪随机监测了200辆汽车的时速,得到如下频数分布表(不完整):注:30-40为时速大于或等于30千米而小于40千米,其它类同.| 数据段 | 频数 |
| 30~40 | 10 |
| 40~50 | 36 |
| 50~60 | 80 |
| 60~70 | 54 |
| 70~80 | 20 |
(2)补全频数分布直方图;
(3)如果此路段该时间段经过的车有1000辆.估计约有多少辆车的时速大于或等于 60千米.
18.已知a-b=3,b-c=-4,则代数式a2-ac-b(a-c)的值为( )
| A. | 4 | B. | -4 | C. | 3 | D. | -3 |
 如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为m的大正方形,两块是边长都为n的小正方形,五块是长为m,宽为n的全等小矩形,且m>n.(以上长度单位:cm)
如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为m的大正方形,两块是边长都为n的小正方形,五块是长为m,宽为n的全等小矩形,且m>n.(以上长度单位:cm)