化简(1)$\sqrt{\frac{49a}{64{b}^{2}}}$(2)$\sqrt{\frac{0.01×81}{0.25×144}}$．题目和参考答案——青夏教育精英家教网—

题目内容

3．化简
（1）$\sqrt{\frac{49a}{64{b}^{2}}}$（a＞0，b＜0）
（2）$\sqrt{\frac{0.01×81}{0.25×144}}$．

分析根据二次根式的性质，可得答案．

解答解：（1）原式=$\frac{\sqrt{{7}^{2}a}}{\sqrt{{8}^{2}•（-{b）}^{2}}}$=$\frac{7\sqrt{a}}{8b}$；
（2）原式=$\frac{\sqrt{0.01}×\sqrt{81}}{\sqrt{0.25}×\sqrt{144}}$=$\frac{0.1×9}{0.5×12}$=$\frac{3}{20}$．

点评本题考查了二次根式的性质，利用二次根式的性质是解题关键．

练习册系列答案

相关题目

14．若y₁=-x+3，y₂=3x-4，回答下列问题：
（1）当x取何值时，y₁=y₂；
（2）当x取何值时，y₁＞y₂；
（3）当x取何值时，y₁＜y₂．

11．

如图，∠B=62°，∠1=62°，∠D=36°．
（1）试说明AB∥CD；
（2）求∠A的度数．

18．

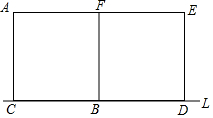如图，已知边长等于8个单位长度的两个完全相同的正方形ACBF、BDEF有公共边BF，且CB与BD均在直线L上，将正方形ACBF沿直线L以1单位/秒向右平移，设移动时间为t秒，正方形ACBF在移动过程中与正方形BDEF重叠的面积为S，试求：
（1）当点B移动到线段BD上时，写出S与t的函数解析式，并写出定义域．
（2）在整个移动过程中，当点C移动到线段BD上时（不与B、D重合），写出S与t的函数解析式，并写出定义域．

8．已知两直线l₁：y=k₁x+b₁，l₂：y=k₂x+b₂，若l₁⊥l₂，则有k₁•k₂=-1，若直线经过A（2，3），且与y=-$\frac{1}{3}$x+3垂直，求该直线的表达式．

15．

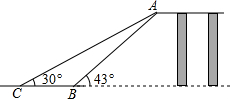如图是某工厂货物传送带的平面示意图，为提高传送过程的安全性，工厂计划改造传动带与地面的夹角，使其AB的坡角由原来的43°改为30°．已知原传送带AB长为5米．求新旧货物传送带着地点B、C之间相距多远？（结果保留整数，参考数据：sin43°≈0.68，cos43°≈0.73，tan43°≈0.93，$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73）

12．

如图，直线AB、CD相交于点O，若∠EOD=40°，∠BOC=130°，那么射线OE与直线AB的位置关系是互相垂直．

13．计算：（-1）^-1+（$\frac{1}{3}$）^-2×2^-2-（-$\frac{1}{2}$）²×（π-3.14）⁰．

试题分类