题目内容
8.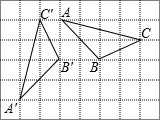 如图,在正方形网格中,每个小正方形的边长均为1,△ABC和△A′B′C′的各个顶点均在格点处,且△A′B′C′是由△ABC以网格中的某个格点为旋转中心,逆时针旋转90°得到的,点A,B,C的对应点分别为点A′,B′,C′,则在旋转过程中,点A经过的路径长为( )
如图,在正方形网格中,每个小正方形的边长均为1,△ABC和△A′B′C′的各个顶点均在格点处,且△A′B′C′是由△ABC以网格中的某个格点为旋转中心,逆时针旋转90°得到的,点A,B,C的对应点分别为点A′,B′,C′,则在旋转过程中,点A经过的路径长为( )| A. | $\frac{\sqrt{10}}{4}$π | B. | $\frac{\sqrt{13}}{2}$π | C. | $\frac{\sqrt{13}}{4}$π | D. | $\frac{\sqrt{10}}{2}$π |
分析 确定旋转中心,旋转角、旋转半径即可解决问题.
解答 解:如图旋转中心为O,旋转角为90°,旋转半径为$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∴点A经过的路径长为$\frac{90•π•\sqrt{10}}{180}$=$\frac{\sqrt{10}}{2}$π,
故选D.
点评 本题考查轨迹、旋转变换、弧长公式等知识,解题的关键是确定旋转中心,旋转角、旋转半径.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
19.若关于x、y的方程ax-2y=-4有一组解$\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$,则a的值为( )
| A. | -8 | B. | 6 | C. | -5 | D. | 7 |
16.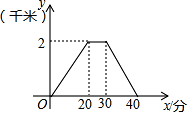 某天,小王去朋友家借书,在朋友家停留一段时间后,返回家中,如图是他离家的路程y(千米)与时间x(分)关系的图象,根据图象信息,下列说法正确的是( )
某天,小王去朋友家借书,在朋友家停留一段时间后,返回家中,如图是他离家的路程y(千米)与时间x(分)关系的图象,根据图象信息,下列说法正确的是( )
 某天,小王去朋友家借书,在朋友家停留一段时间后,返回家中,如图是他离家的路程y(千米)与时间x(分)关系的图象,根据图象信息,下列说法正确的是( )
某天,小王去朋友家借书,在朋友家停留一段时间后,返回家中,如图是他离家的路程y(千米)与时间x(分)关系的图象,根据图象信息,下列说法正确的是( )| A. | 小王去时的速度大于回家的速度 | |
| B. | 小王去时走上坡路,回家时走下坡路 | |
| C. | 小王去时所花时间少于回家所花时间 | |
| D. | 小王在朋友家停留了10分 |
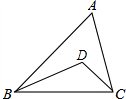 在△ABC中,∠A=50°,D点时∠ABC和∠ACB角平分线的交点,则∠BDC=115°.
在△ABC中,∠A=50°,D点时∠ABC和∠ACB角平分线的交点,则∠BDC=115°.