题目内容
3. 如图,若将面积为4cm2的矩形木框变为?ABCD的形状,并使平行四边形的最小内角为30°,则?ABCD的面积为2cm2.
如图,若将面积为4cm2的矩形木框变为?ABCD的形状,并使平行四边形的最小内角为30°,则?ABCD的面积为2cm2.
分析 作AE⊥BC于E,则∠AEB=90°,由∠ABC=30°,得出AE=$\frac{1}{2}$AB,?ABCD的面积=BC•AE=$\frac{1}{2}$BC•AB,即可得出结果.
解答 解:作AE⊥BC于E,如图所示: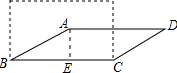 则∠AEB=90°,
则∠AEB=90°,
∵∠ABC=30°,
∴AE=$\frac{1}{2}$AB,
∴?ABCD的面积=BC•AE=$\frac{1}{2}$BC•AB?$\frac{1}{2}$×4=2(cm2),
故答案为:2.
点评 本题考查了矩形的性质、平行四边形的性质、含30°角的直角三角形的性质;熟练掌握矩形的性质和平行四边形的性质,并能进行推理计算是即为的关键.

练习册系列答案
相关题目
13. 下列平面图形绕虚线旋转一周能形成如图立体图形的是( )
下列平面图形绕虚线旋转一周能形成如图立体图形的是( )
 下列平面图形绕虚线旋转一周能形成如图立体图形的是( )
下列平面图形绕虚线旋转一周能形成如图立体图形的是( )| A. |  | B. |  | C. |  | D. |  |
 如图,在△ABC中,D,E,F分别为BC,AD,CE的中点,且S△ABC=8cm2,求阴影部分的面积.
如图,在△ABC中,D,E,F分别为BC,AD,CE的中点,且S△ABC=8cm2,求阴影部分的面积.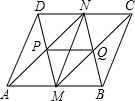 如图,在?ABCD中,M,N分别是AB,CD的中点,AN和DM相交于点P,BN和CM相交于点Q,请思考下列问题:
如图,在?ABCD中,M,N分别是AB,CD的中点,AN和DM相交于点P,BN和CM相交于点Q,请思考下列问题: 如图,在△ABC中,AB=AC,作出此三角形的中线AD,高线AE,角平分线AF,你能得到什么结论?多画几个符合要求而不同的图形验证一下你的结论.
如图,在△ABC中,AB=AC,作出此三角形的中线AD,高线AE,角平分线AF,你能得到什么结论?多画几个符合要求而不同的图形验证一下你的结论. 如图,在梯形ABCD中,AB∥CD,AB=15,CD=30,点E,F分别为AD,BC上一点,且EF∥AB.若梯形AEFB∽梯形EDCF,求线段EF的长.
如图,在梯形ABCD中,AB∥CD,AB=15,CD=30,点E,F分别为AD,BC上一点,且EF∥AB.若梯形AEFB∽梯形EDCF,求线段EF的长.