题目内容
8．
如图，在梯形ABCD中，AB∥CD，AB=15，CD=30，点E，F分别为AD，BC上一点，且EF∥AB．若梯形AEFB∽梯形EDCF，求线段EF的长．
分析 根据相似多边形对应边成比例列出关系式，代入已知数据计算即可．
解答 解：∵AEFB∽梯形EDCF，
∴$\frac{AB}{EF}$=$\frac{EF}{CD}$，
∴EF2=AB×CD=450，
解得EF=15$\sqrt{2}$．
点评 本题考查的是相似多边形的性质，掌握相似多边形对应边成比例是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
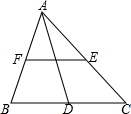如图，EF为△ABC的中位线，AD为BC边上的中线．请从点A，B，C，D，E，F中选出四个点，使以这四个点为顶点的四边形为平行四边形（要求至少找出三个平行四边形）．
如图，在菱形ABCD中，点E是边AD的中点，EF⊥AC，交AB边于G，交CB的延长线于点F，求证：AB与EF互相平分．
如图，若将面积为4cm2的矩形木框变为?ABCD的形状，并使平行四边形的最小内角为30°，则?ABCD的面积为2cm2．
如图，在△ABC中，∠DAB=∠C，∠B的平分线BN交AD于M．求证：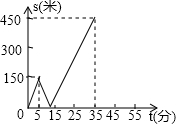
甲乙两人匀速从同一地点到1500米处的图书馆看书，甲出发5分钟后，乙出发沿同一路线行走．设甲乙两人相距s（米），甲行走的时间为t（分），s关于t的函数函数图象的一部分如图所示，下列说法：