题目内容
15.如图1,在菱形ABDE与菱形ACGF中,∠BDE=∠AFG,M为BC中点,直线AM交EF于N,探索∠ANF与∠BDE的数量关系,并证明你的结论.(说明:如果你反复探索没有解决问题,可以补充∠BDE=90°的条件完成解答(如图2)).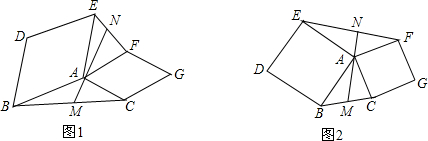
分析 延长AM到P,使PM=AM,连接PC,得到△ABM≌△PCM,于是推出∠2=∠P,AB=CP,得到AB∥CP,根据平行线的性质得到∠BAC+∠ACP=180°,在菱形ABDE与菱形ACGF中,由于∠BDF=∠AFG,∠BDF=∠BAE,∠AFC+∠FAC=180°,于是得到∠BAE+∠FAC=180°,证得∠ACP=∠EAF,证出△APC≌△FEA,得到∠AEF=∠P,由于∠ANF=∠ANE+∠1,∠AEN=∠P=∠2,于是得到∠ANF=∠2+∠1=180°-∠BAE,即∠ANF=180°-∠BDE,结论即可得到.
解答 解:延长AM到P,使PM=AM,连接PC,
在△ABM与△CPM中,
$\left\{\begin{array}{l}{AM=PM}\\{∠AMB=∠PMC}\\{BM=CM}\end{array}\right.$,
∴△ABM≌△PCM,
∴∠2=∠P,AB=CP,
∴AB∥CP,
∴∠BAC+∠ACP=180°,
在菱形ABDE与菱形ACGF中,
∵∠BDE=∠AFG,∠BDE=∠BAE,∠AFC+∠FAC=180°,
∴∠BAE+∠FAC=180°, ∴∠EAF+∠BAC=360°-(∠BAE+∠FAC)=180°,
∴∠EAF+∠BAC=360°-(∠BAE+∠FAC)=180°,
∴∠ACP=∠EAF.
在△APC与△FEA中,
$\left\{\begin{array}{l}{PC=EA}\\{∠ACP=∠FAE}\\{AC=FA}\end{array}\right.$,
∴△APC≌△FEA,
∴∠P=∠FEA,
∵∠ANF=∠AEN+∠1,∠AEN=∠P=∠2,
∴∠ANF=∠2+∠1=180°-∠BAE,即∠ANF=180°-∠BDE,
∴∠ANF+∠BDE=180°,
即∠ANF与∠BDE互补.
点评 本题考查了菱形的性质,全等三角形的判定与性质,证明出∠AEN=∠P=∠2是解此题的关键.

 如图,若将面积为4cm2的矩形木框变为?ABCD的形状,并使平行四边形的最小内角为30°,则?ABCD的面积为2cm2.
如图,若将面积为4cm2的矩形木框变为?ABCD的形状,并使平行四边形的最小内角为30°,则?ABCD的面积为2cm2. 已知直线y=3x+3与x轴交于点A,与y轴交于点D,与直线y=$\frac{3}{4}$x交于点E.过点D作DC∥x轴,交直线y=$\frac{3}{4}$x于点C,过点C作CB∥AD交x轴于点B.点P从点O出发,沿线段OC向终点C运动,点Q从点C出发,沿线段CD向终点D运动.若P、Q同时出发,速度均为1单位长度/s,时间为t s.当P、Q两点有一点到达终点时,它们均停止运动.将线段PQ绕点P沿顺时针方向旋转90°.当点Q落在四边形ABCD一边所在的直线上时,t的值为2.
已知直线y=3x+3与x轴交于点A,与y轴交于点D,与直线y=$\frac{3}{4}$x交于点E.过点D作DC∥x轴,交直线y=$\frac{3}{4}$x于点C,过点C作CB∥AD交x轴于点B.点P从点O出发,沿线段OC向终点C运动,点Q从点C出发,沿线段CD向终点D运动.若P、Q同时出发,速度均为1单位长度/s,时间为t s.当P、Q两点有一点到达终点时,它们均停止运动.将线段PQ绕点P沿顺时针方向旋转90°.当点Q落在四边形ABCD一边所在的直线上时,t的值为2.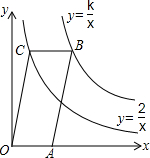 如图,已知点A在x轴上,?OABC的顶点B在反比例函数y=$\frac{k}{x}$的图象上,顶点C在反比例函数y=$\frac{2}{x}$的图象上,?OABC的面积等于4.
如图,已知点A在x轴上,?OABC的顶点B在反比例函数y=$\frac{k}{x}$的图象上,顶点C在反比例函数y=$\frac{2}{x}$的图象上,?OABC的面积等于4. 如图,O是直线AB上的任一点,且OC⊥OD,∠1=35°,则∠2=55度.
如图,O是直线AB上的任一点,且OC⊥OD,∠1=35°,则∠2=55度.