题目内容
20. 如图,在△ABC中,∠BAC=90°,∠B=60°,AD⊥BC于点D,则△ABD与△ADC的面积比为1:3.
如图,在△ABC中,∠BAC=90°,∠B=60°,AD⊥BC于点D,则△ABD与△ADC的面积比为1:3.
分析 根据∠BAC=90°,可得∠BAD+∠CAD=90°,再根据垂直的定义得到∠ADB=∠CDA=90°,利用三角形的内角和定理可得∠B+∠BAD=90°,根据同角的余角相等得到∠B=∠CAD,利用两对对应角相等两三角形相似得到△ABD∽△CAD,由tanB=tan60°=$\frac{AD}{BD}$=$\sqrt{3}$,再根据相似三角形的面积比等于相似比(对应边的之比)的平方即可求出结果.
解答 解:∵∠BAC=90°,
∴∠BAD+∠CAD=90°,
又∵AD⊥BC,
∴∠ADB=∠CDA=90°,
∴∠B+∠BAD=90°,
∴∠B=∠CAD,又∠ADB=∠CDA=90°,
∴△ABD∽△CAD,
∴$\frac{{S}_{△ABD}}{{S}_{△CAD}}$=($\frac{AB}{AC}$)2,
∵∠B=60°,
∴$\frac{AB}{AC}$=$\frac{\sqrt{3}}{3}$,
∴$\frac{{S}_{△ABD}}{{S}_{△CAD}}$=($\frac{AB}{AC}$)2=$\frac{1}{3}$.
故答案为:1:3.
点评 此题考查了相似三角形的判定与性质,熟练掌握相似比即为对应边之比,周长比等于相似比,面积之比等于相似比的平方是解决问题的关键.

练习册系列答案
相关题目
15.“创建国家森林城市,打造秀美、和谐祁阳.”某乡镇组织300名干部、群众参加义务植树活动,下表是随机抽出的50名干部、群众义务植树的统计,根据图中的数据回答下列问题:
(1)这50个人平均每人植树4.8棵;
(2)植树棵数的中位数是4.5棵;
(3)植树棵数的众数是4棵;
(4)估计该乡镇本次活动共植树1440棵.
| 植树棵树 | 3 | 4 | 5 | 6 | 8 |
| 人 数 | 10 | 15 | 12 | 7 | 6 |
(2)植树棵数的中位数是4.5棵;
(3)植树棵数的众数是4棵;
(4)估计该乡镇本次活动共植树1440棵.
15.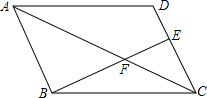 如图,在平行四边形ABCD中,点E在CD上,若DE:CE=1:2,则△CEF与△ABF的周长比为( )
如图,在平行四边形ABCD中,点E在CD上,若DE:CE=1:2,则△CEF与△ABF的周长比为( )
 如图,在平行四边形ABCD中,点E在CD上,若DE:CE=1:2,则△CEF与△ABF的周长比为( )
如图,在平行四边形ABCD中,点E在CD上,若DE:CE=1:2,则△CEF与△ABF的周长比为( )| A. | 1:2 | B. | 1:3 | C. | 2:3 | D. | 4:9 |
 如图,点A在数轴上对应的数为2,若点B也在数轴上,且线段AB的长为4,C为OB的中点,则点C在数轴上对应的数为-1或3.
如图,点A在数轴上对应的数为2,若点B也在数轴上,且线段AB的长为4,C为OB的中点,则点C在数轴上对应的数为-1或3.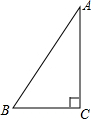 (1)如图,△ABC是直角三角形,∠ACB=90°,利用直尺和圆规,按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
(1)如图,△ABC是直角三角形,∠ACB=90°,利用直尺和圆规,按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)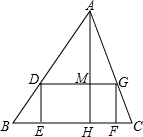 如图,四边形DEFG是△ABC的内接矩形,如果△ABC的高线AH长8cm,底边BC长10cm,设DG=xcm,DE=ycm,
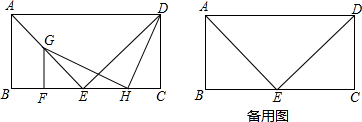
如图,四边形DEFG是△ABC的内接矩形,如果△ABC的高线AH长8cm,底边BC长10cm,设DG=xcm,DE=ycm,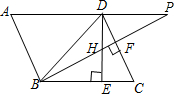 如图,在平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线交于P.下面结论:
如图,在平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线交于P.下面结论: