题目内容
12.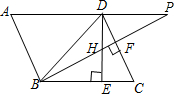 如图,在平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线交于P.下面结论:
如图,在平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线交于P.下面结论:①$DB=\sqrt{2}BE$,②∠A=∠BHE,③AB=BH,④△BHD∽△BDP.
请你把你认为正确的结论的番号都填上①②③ (填错一个该题得0分)
分析 通过判断△BDE为等腰直角三角形,得到BE=DE,BD=$\sqrt{2}$BE,则可对①进行判断;根据等角的余角相等得到∠BHE=∠C,再根据平行四边形的性质得到∠A=∠C,则∠A=∠BHE,于是可对②进行判断;根据“AAS”可证明△BEH≌△DEC,得到BH=CD,接着由平行四边形的性质得AB=CD,则AB=BH,运算可对③进行判断;利用平行线的性质可得AP∥BC,则∠ADP=∠DBC=45°,利用三角形外角性质得∠P<45°,而∠BDH=45°,加上△BHD与△BDP有一个公共角,则可判断△BHD与△BDP不相似,于是可对④进行判断;
解答 解:∵∠DBC=45°,DE⊥BC,
∴△BDE为等腰直角三角形,
∴BE=DE,BD=$\sqrt{2}$BE,所以①正确;
∵BF⊥CD,
∴∠C+∠CBF=90°,
而∠BHE+∠CBF=90°,
∴∠BHE=∠C,
∵四边形ABCD为平行四边形,
∴∠A=∠C,
∴∠A=∠BHE,所以②正确;
在△BEH和△DEC中,
$\left\{\begin{array}{l}{∠BHE=∠C}\\{∠HEB=∠CED}\\{BE=DE}\end{array}\right.$,
∴△BEH≌△DEC,
∴BH=CD
∵四边形ABCD为平行四边形,
∴AB=CD,
∴AB=BH,所以③正确;
∵AP∥BC,
∴∠ADP=∠DBC=45°,
∴∠BDP=135°,
∴∠P<45°,
而∠BDH=45°,
∴∠BDGP≠∠P,
∴△BHD与△BDP不相似,所以④错误;
∴正确的有①②③;
故答案为:①②③.
点评 本题考查了平行四边形的性质和相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.

 名校课堂系列答案
名校课堂系列答案| A. | x=-2 | B. | x=0 | C. | $x=-\frac{1}{2}$ | D. | $x=\frac{1}{2}$ |
| A. | 若方程有一根为1,则a+b+c=0 | B. | 若a、c异号,则方程必有解 | ||
| C. | 若b=0,则方程两根互为相反数 | D. | 若c=0,则方程有一根为0 |
| A. | $\sqrt{41}$ | B. | 3 | C. | 3或$\sqrt{41}$ | D. | 以上都不对 |
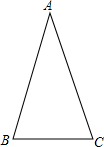 已知,如图,△ABC中,AB=AC,∠A=36°,你能否剪两刀将△ABC分成三个等腰三角形,请将剪痕画在三角形中(至少画出两种剪法,并在图上标出各个角的度数).
已知,如图,△ABC中,AB=AC,∠A=36°,你能否剪两刀将△ABC分成三个等腰三角形,请将剪痕画在三角形中(至少画出两种剪法,并在图上标出各个角的度数). 如图,在△ABC中,∠BAC=90°,∠B=60°,AD⊥BC于点D,则△ABD与△ADC的面积比为1:3.
如图,在△ABC中,∠BAC=90°,∠B=60°,AD⊥BC于点D,则△ABD与△ADC的面积比为1:3.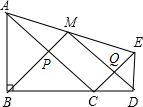 如图,△ABC和△CDE均为等腰直角三角形,点B、C、D在一条直线上,点M是AE的中点,给出下列结论:
如图,△ABC和△CDE均为等腰直角三角形,点B、C、D在一条直线上,点M是AE的中点,给出下列结论: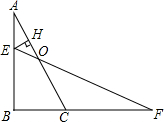 如图,在直角三角形ABC中,点E在线段AB上,过点E作EH⊥AC交AC于点H,点F在BC的延长线上,连结EF交AC于点O.若AB=2,BC=1,且$\frac{CF}{AE}=2$,则$\frac{OE}{OF}$=$\frac{1}{4}$,OH=$\frac{\sqrt{5}}{5}$.
如图,在直角三角形ABC中,点E在线段AB上,过点E作EH⊥AC交AC于点H,点F在BC的延长线上,连结EF交AC于点O.若AB=2,BC=1,且$\frac{CF}{AE}=2$,则$\frac{OE}{OF}$=$\frac{1}{4}$,OH=$\frac{\sqrt{5}}{5}$.