题目内容
3.如图1,在△ABC中,D、E、F分别为三边的中点,G点在AB边上,△BDG与四边形ACDG的周长相等.(1)求证:BG=AG+AC;
(2)求证:∠BGD=$\frac{1}{2}∠A$;
(3)如图2,连接CG交DE于点H,若BG⊥CG,探索线段DG、DH、AC之间满足的关系式.
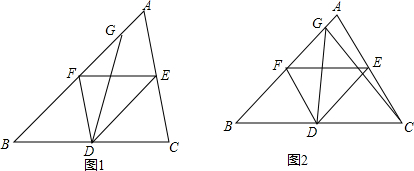
分析 (1)根据周长相等,列出等式即可证明.
(2)想办法证明FG=FD,得到∠FGD=∠FDG,∠A=∠BFD,由此即可证明.
(3)结论;DG2=AC•DH,:作FM⊥DG于M,只要证明△DFM∽△DGH,得到$\frac{DF}{DG}$=$\frac{DM}{DH}$,用DF=$\frac{1}{2}$AC.DM=$\frac{1}{2}$DG代入即可解决问题.
解答 (1)证明: ∵△BDG与四边形ACDG的周长相等,
∵△BDG与四边形ACDG的周长相等,
∴BD+DG+BG=BG+AG+AC+CD,
∵BD=DC,
∴BG=AG+AC.
(2)证明:∵BF=AF,BD=DC,
∴DF∥AC,DF=$\frac{1}{2}$AC,
∴∠BFD=∠A,
∵BG=AG+AC,
∴BG=AB-BG+AC,
∴2BG=AB+AC,
∴BG=$\frac{1}{2}$AB+$\frac{1}{2}$AC,
∴BG=BF+DF=BF+FG,
∴DF=FG,
∴∠FGD=∠FDG,
∵∠BFD=∠FGD+∠FDG=2∠FGD,
∴∠A=2∠FGD,
∴∠FGD=$\frac{1}{2}$∠A.
(3)结论:DG2=AC•DH,理由:
证明:作FM⊥DG于M,
∵FD=FG(已证),
∴∠FGD=∠FDG,DM=GM,
∵BD=DC,AE=EC,
∴DE∥AB,
∴∠FGD=∠GDH,
∴∠FDM=∠GDH,
∵∠FMD=∠GHD=90°,
∴△DFM∽△DGH,
∴$\frac{DF}{DG}$=$\frac{DM}{DH}$,
∴$\frac{\frac{1}{2}AC}{DG}$=$\frac{\frac{1}{2}DG}{DH}$,
∴DG2=AC•DH.
补充方法:△FGD∽△DGB得到DG2=FG•BG,FG=$\frac{1}{2}$AC,BG=2DH得DG2=AC•DH.
点评 本题考查三角形中位线定理、相似三角形的判定和性质、等腰三角形的判定和性质等知识,解题的关键是添加辅助线,构造相似三角形,属于中考常考题型.

| A. | 垂线段最短 | B. | 两直线平行,同旁内角相等 | ||
| C. | 对顶角相等 | D. | 两点之间,线段最短 |
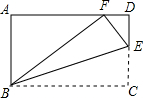 如图,在矩形ABCD中,E为CD边上的点,将△BCE沿BE折叠,点C恰好落在AD边上的点F处.
如图,在矩形ABCD中,E为CD边上的点,将△BCE沿BE折叠,点C恰好落在AD边上的点F处. 如图,?ABCD的对角线AC,BD相交于点O,点E是边AD的中点,若△BCD的周长为18,则△DEO的周长是9.
如图,?ABCD的对角线AC,BD相交于点O,点E是边AD的中点,若△BCD的周长为18,则△DEO的周长是9.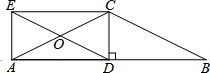 如图,CD垂直平分AB于点D,连接CA,CB,将BC沿BA的方向平移,得到线段DE,交AC于点O,连接EA,EC.
如图,CD垂直平分AB于点D,连接CA,CB,将BC沿BA的方向平移,得到线段DE,交AC于点O,连接EA,EC.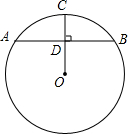 如图,在⊙O中,AB为⊙O的弦,半径OC⊥AB于点D,若OB的长为10,sin∠BOD=$\frac{4}{5}$,则AB的长为16.
如图,在⊙O中,AB为⊙O的弦,半径OC⊥AB于点D,若OB的长为10,sin∠BOD=$\frac{4}{5}$,则AB的长为16.