题目内容
18．
如图，?ABCD的对角线AC，BD相交于点O，点E是边AD的中点，若△BCD的周长为18，则△DEO的周长是9．
分析 根据平行四边形的性质得出DE=$\frac{1}{2}$AD=$\frac{1}{2}$BC，DO=$\frac{1}{2}$BD，AO=CO，求出OE=$\frac{1}{2}$CD，求出△DEO的周长是DE+OE+DO=$\frac{1}{2}$（BC+DC+BD），代入求出即可．
解答 解：∵E为AD中点，四边形ABCD是平行四边形，
∴DE=$\frac{1}{2}$AD=$\frac{1}{2}$BC，DO=$\frac{1}{2}$BD，AO=CO，
∴OE=$\frac{1}{2}$CD，
∵△BCD的周长为18，
∴BD+DC+BC=18，
∴△DEO的周长是DE+OE+DO=$\frac{1}{2}$（BC+DC+BD）=$\frac{1}{2}$×18=9，
故答案为：9．
点评 本题考查了平行四边形的性质，三角形的中位线的应用，解此题的关键是求出DE=$\frac{1}{2}$BC，DO=$\frac{1}{2}$BD，OE=$\frac{1}{2}$DC．
练习册系列答案
相关题目
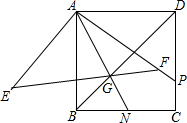已知：如图，正方形ABCD中，把△ABD绕点A旋转得到△AEF，EF、BD相交于点G，连接AG并延长交BC于N，延长AF交CD于点P，若NC=2，AP=5，则AG的长为$\frac{4\sqrt{3}}{3}$．
9．
如图，在△ABC中，AB=5，AC=12，点D，E，F分别是AB，BC，AC的中点，则四边形ADEF的周长为（ ）
如图，在△ABC中，AB=5，AC=12，点D，E，F分别是AB，BC，AC的中点，则四边形ADEF的周长为（ ）| A． | 10 | B． | 12 | C． | 13 | D． | 17 |
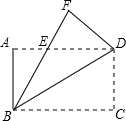如图，把矩形ABCD沿对角线BD折叠使点C落在F处，BF交AD于点E．