题目内容
8.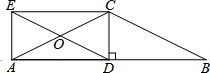 如图,CD垂直平分AB于点D,连接CA,CB,将BC沿BA的方向平移,得到线段DE,交AC于点O,连接EA,EC.
如图,CD垂直平分AB于点D,连接CA,CB,将BC沿BA的方向平移,得到线段DE,交AC于点O,连接EA,EC.(1)求证:四边形ADCE是矩形;
(2)若CD=1,AD=2,求sin∠COD的值.
分析 (1)根据“有一内角为直角的平行四边形为矩形”进行证明即可;
(2)如图,过D作DF⊥AC于F,利用矩形的对角线相互平分的性质、勾股定理求得OD的长度;然后利用面积法可以求得DF的长度,所以通过解Rt△ODF得到答案.
解答 (1)证明:由已知得BD∥CE,BD=CE.
∵CD垂直平分AB,
∴AD=BD,∠CDA=90°.
∵结合平移的性质得到:AD∥CE,AD=CE.
∴四边形ADCE是平行四边形,
∴平行四边形ADCE是矩形;
(2)解:过D作DF⊥AC于F, 在Rt△ADC中,∠CDA=90°,
在Rt△ADC中,∠CDA=90°,
∵CD=1,AD=2,
由勾股定理可得:AC=$\sqrt{5}$.
∵O为AC中点,
∴OD=$\frac{{\sqrt{5}}}{2}$.
∵AC•DF=AD•DC,
∴DF=$\frac{{2\sqrt{5}}}{5}$.
在Rt△ODF中,∠OFD=90°,
∴sin∠COD=$\frac{DF}{OD}$=$\frac{4}{5}$.
点评 本题考查了勾股定理,矩形的性质以及平移的性质.解答(2)时,辅助线的作法和求法是解题的难点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.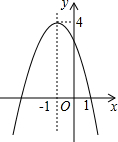 如图是二次函数:y=ax2+bx+c(a≠0)的图象,下列说法错误的是( )
如图是二次函数:y=ax2+bx+c(a≠0)的图象,下列说法错误的是( )
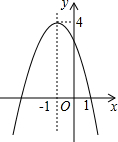 如图是二次函数:y=ax2+bx+c(a≠0)的图象,下列说法错误的是( )
如图是二次函数:y=ax2+bx+c(a≠0)的图象,下列说法错误的是( )| A. | 函数y的最大值是4 | B. | 函效的图象关于直线x=-1对称 | ||
| C. | 当x<-1时,y随x的增大而增大 | D. | 当-4<x<1时,函数值y>0 |




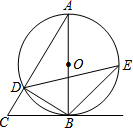 如图,已知△ABC,以AB为直径的⊙O交AC于点D,∠CBD=∠A.
如图,已知△ABC,以AB为直径的⊙O交AC于点D,∠CBD=∠A.