题目内容
16. (1)尺规作图:作△ABC的外接圆⊙O.(保留作图痕迹,不写画法)
(1)尺规作图:作△ABC的外接圆⊙O.(保留作图痕迹,不写画法)(2)若∠A=45°,⊙O的半径为1,求BC的长.
(3)求所作的⊙O中弧BC和弦BC围成的区域面积.
分析 (1)分别作AB和BC的垂直平分线,两垂直平分线相交于点0,然后以O点为圆心,OB为半径作圆即可;
(2)连结OB,OC,根据圆周角定理得到∠BOC=2∠A=90°,于是可判断△OBC是等腰直角三角形,然后根据等腰直角三角形的性质求解;
(3)利用S弓形BC=S扇形BOC-S△BOC可得.
解答 解:(1)如图,⊙O为所作;
(2)连结OB,OC,
∵∠A=45
∴∠BOC=2∠A=90°
又∵OB=OC=1,
∴△OBC是等腰直角三角形,
∴BC=$\sqrt{2}$OB=$\sqrt{2}$;
(3)S弓形BC=S扇形BOC-S△BOC=$\frac{90•π•{1}^{2}}{360}$-$\frac{1}{2}$×1×1=$\frac{π-2}{4}$.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了圆周角定理.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
6.将函数y=-2x的图象沿y轴向上平移3个单位长度后,所得图象对应的函数表达式为( )
| A. | y=x | B. | y=-2x+3 | C. | y=-2x-3 | D. | y=-2(x+3) |
7.用四舍五人法按要求把2.05446取近似值,其中错误的是( )
| A. | 2.1(精确到0.1) | B. | 2.05(精确到百分位) | ||
| C. | 2.054(精确到0.001) | D. | 2.0544(精确到万分位) |
 甲、乙两人同在如图所示的地下车库等电梯,两人到1至4层的任意一层出电梯,
甲、乙两人同在如图所示的地下车库等电梯,两人到1至4层的任意一层出电梯,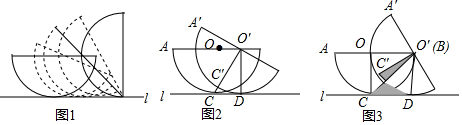 如图1,一个半径为2的半圆在平面作无滑动顺时针滚动,可以把平面看做直线l,初始位置的半圆O与直线l相切于点C,AB∥l,滚动过程中,半圆O′与直线l相切于点D,点A、B、C在半圆O′上的对应点分别为A′、B′、C′.
如图1,一个半径为2的半圆在平面作无滑动顺时针滚动,可以把平面看做直线l,初始位置的半圆O与直线l相切于点C,AB∥l,滚动过程中,半圆O′与直线l相切于点D,点A、B、C在半圆O′上的对应点分别为A′、B′、C′. 如图.已知二次函数y=ax2+bx(α≠0)经过点A(-2,0),B(-3,3).
如图.已知二次函数y=ax2+bx(α≠0)经过点A(-2,0),B(-3,3).