题目内容
7.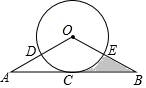 如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E,$\widehat{CD}$=$\widehat{CE}$
如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E,$\widehat{CD}$=$\widehat{CE}$(1)求证:OA=OB;
(2)已知AB=4$\sqrt{3}$,OA=4,求阴影部分的面积.
分析 (1)连接OC,由切线的性质可知∠ACO=90°,由于$\widehat{CD}$=$\widehat{CE}$,所以∠AOC=∠BOC,从而可证明∠A=∠B,从而可知OA=OB;
(2)由(1)可知:△AOB是等腰三角形,所以AC=2$\sqrt{3}$,从可求出扇形OCE的面积以及△OCB的面积
解答 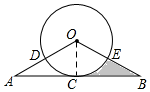 解:(1)连接OC,
解:(1)连接OC,
∵AB与⊙O相切于点C
∴∠ACO=90°,
由于$\widehat{CD}$=$\widehat{CE}$,
∴∠AOC=∠BOC,
∴∠A=∠B
∴OA=OB,
(2)由(1)可知:△OAB是等腰三角形,
∴BC=$\frac{1}{2}$AB=2$\sqrt{3}$,
∴sin∠COB=$\frac{BC}{OB}$=$\frac{\sqrt{3}}{2}$,
∴∠COB=60°,
∴∠B=30°,
∴OC=$\frac{1}{2}$OB=2,
∴扇形OCE的面积为:$\frac{60π×4}{360}$=$\frac{2π}{3}$,
△OCB的面积为:$\frac{1}{2}$×2$\sqrt{3}$×2=2$\sqrt{3}$
∴S阴影=2$\sqrt{3}$-$\frac{2}{3}$π
点评 本题考查切线的性质,解题的关键是求证OA=OB,然后利用等腰三角形的三线合一定理求出BC与OC的长度,从而可知扇形OCE与△OCB的面积,本题属于中等题型.

练习册系列答案
 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
15. 某几何体的三视图如图所示,因此几何体是( )
某几何体的三视图如图所示,因此几何体是( )
 某几何体的三视图如图所示,因此几何体是( )
某几何体的三视图如图所示,因此几何体是( )| A. | 长方形 | B. | 圆柱 | C. | 球 | D. | 正三棱柱 |
12.若一个三角形的两边长分别为5和8,则第三边长可能是( )
| A. | 14 | B. | 10 | C. | 3 | D. | 2 |
4.明星队参加“希望杯”篮球比赛,在前8场比赛中的部分积分情况如表:
(1)求本次比赛中,胜一场和负一场各积多少分?
(2)前8场比赛结束时,某队是否存在胜场总积分等于它的负场总积分的情况?为什么?
(3)8场比赛以后还剩余m场比赛,当比赛结束时,该队是否存在胜场总积分等于它的负场总积分的情况?如果存在,求出胜场场次;如果不存在,请说明理由.
| 比赛场次 | 胜场 | 负场 | 积分 |
| m | 0 | m | m |
| 8 | 3 | 5 | 11 |
(2)前8场比赛结束时,某队是否存在胜场总积分等于它的负场总积分的情况?为什么?
(3)8场比赛以后还剩余m场比赛,当比赛结束时,该队是否存在胜场总积分等于它的负场总积分的情况?如果存在,求出胜场场次;如果不存在,请说明理由.
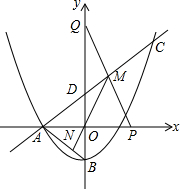 如图,抛物线y=$\frac{1}{4}$x2+$\frac{1}{4}$x+c与x轴的负半轴交于点A,与y轴交于点B,连结AB,点C(6,$\frac{15}{2}}$)在抛物线上,直线AC与y轴交于点D.
如图,抛物线y=$\frac{1}{4}$x2+$\frac{1}{4}$x+c与x轴的负半轴交于点A,与y轴交于点B,连结AB,点C(6,$\frac{15}{2}}$)在抛物线上,直线AC与y轴交于点D.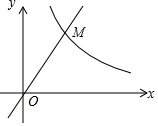 如图,点M是函数y=$\sqrt{3}$x与y=$\frac{k}{x}$的图象在第一象限内的交点,OM=4,则k的值为4$\sqrt{3}$.
如图,点M是函数y=$\sqrt{3}$x与y=$\frac{k}{x}$的图象在第一象限内的交点,OM=4,则k的值为4$\sqrt{3}$. 如图,直线a∥b,∠BAC的顶点A在直线a上,且∠BAC=100°.若∠1=34°,则∠2=46°.
如图,直线a∥b,∠BAC的顶点A在直线a上,且∠BAC=100°.若∠1=34°,则∠2=46°.