Question

4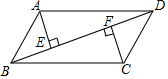．已知：如图，在平行四边形ABCD中，AE⊥BD，CF⊥BD，垂足分别为E，F．求证：△ADE≌△CBF．

Answer 1

分析 指出∠ADE=∠CBF，AD=CB，由AAS证△ADE≌△CBF即可．

解答 证明：∵四边形ABCD是平行四边形，
∴AD=CB，AD∥BC，
∴∠ADE=∠CBF，
∵AE⊥BD，CF⊥BD，
∴∠AED=∠CFB=90°，
在△ADE和△CBF中，$\left\{\begin{array}{l}{∠ADE=∠CBF}&{\;}\\{∠AED=∠CFB}&{\;}\\{AD=CB}&{\;}\end{array}\right.$，
∴△ADE≌△CBF（AAS）．

点评 此题考查了平行四边形的判定与性质、全等三角形的判定与性质．熟练掌握平行四边形的性质是解决问题的关键．