题目内容
1. 平面直角坐标系xOy中,点P的坐标为(m+1,m-1).
平面直角坐标系xOy中,点P的坐标为(m+1,m-1).(1)试判断点P是否在一次函数y=x-2的图象上,并说明理由;
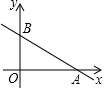
(2)如图,一次函数y=-$\frac{1}{2}$x+3的图象与x轴、y轴分别相交于点A、B,若点P在△AOB的内部,求m的取值范围.
分析 (1)要判断点(m+1,m-1)是否的函数图象上,只要把这个点的坐标代入函数解析式,观察等式是否成立即可.
(2)根据题意得出0<m+1<6,0<m-1<3,m-1<-$\frac{1}{2}$(m+1)+3,解不等式组即可求得.
解答 解:(1)∵当x=m+1时,y=m+1-2=m-1,
∴点P(m+1,m-1)在函数y=x-2图象上.
(2)∵函数y=-$\frac{1}{2}$x+3,
∴A(6,0),B(0,3),
∵点P在△AOB的内部,
∴0<m+1<6,0<m-1<3,m-1<-$\frac{1}{2}$(m+1)+3
∴1<m<$\frac{7}{3}$.
点评 本题考查了一次函数图象上点的坐标特征,一次函数的性质,图象上的点的坐标适合解析式.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
11.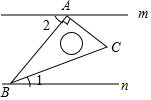 已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,则∠2的度数为( )
已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,则∠2的度数为( )
 已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,则∠2的度数为( )
已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,则∠2的度数为( )| A. | 20° | B. | 30° | C. | 45° | D. | 50° |
12.若一个三角形的两边长分别为5和8,则第三边长可能是( )
| A. | 14 | B. | 10 | C. | 3 | D. | 2 |
9.下列运算正确的是( )
| A. | a3•a3=2a6 | B. | a3+a3=2a6 | C. | (a3)2=a6 | D. | a6•a2=a3 |
6.下列统计量中,反映一组数据波动情况的是( )
| A. | 平均数 | B. | 众数 | C. | 频率 | D. | 方差 |
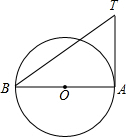 如图,AT切⊙O于点A,AB是⊙O的直径.若∠ABT=40°,则∠ATB=50°.
如图,AT切⊙O于点A,AB是⊙O的直径.若∠ABT=40°,则∠ATB=50°.