题目内容
5.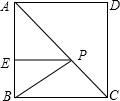 如图,正方形ABCD中,点E在边AB上,且BE=$\sqrt{2}$,AE=3BE,点P在线段AC上的运动,则PE+PB的最小值为5$\sqrt{2}$.
如图,正方形ABCD中,点E在边AB上,且BE=$\sqrt{2}$,AE=3BE,点P在线段AC上的运动,则PE+PB的最小值为5$\sqrt{2}$.
分析 根据线段垂直平分线上的点到线段两端点的距离相等,可得PB=PD,根据两点之间线段最短,可得P点是AC与DE的交点,根据AE=3BE,可得AE的长,根据正方形的性质,可得AD与AB的关系,根据勾股定理,可得答案.
解答 解:如图: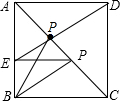 ,
,
由B、D点关于AC对称,得
AC上的点到B的距离等于到D的距离.
连接DE交AC于P,BP=DP.
PE+PB=DE.
由BE=$\sqrt{2}$,AE=3BE,得
AE=3$\sqrt{2}$.
由线段的和差,得
AB=AE+BE=4$\sqrt{2}$.
由正方形的性质,得
AD=AB=4$\sqrt{2}$,∠BAD=90°.
由勾股定理,得
DE=$\sqrt{A{E}^{2}+A{D}^{2}}$=$\sqrt{(3\sqrt{2})^{2}+(4\sqrt{2})^{2}}$=5$\sqrt{2}$,
故答案为:5$\sqrt{2}$.
点评 本题考查了轴对称,利用线段垂直平分线上的点到线段两端点的距离相等得出PB=PD,利用两点之间线段最短得出P点的位置是解题关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
15.在实数:3.141 59,$\root{3}{64}$,1.010 010 001…,4,2.$\stackrel{••}{01}$,2π,$\frac{22}{7}$中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则BC的长是( )
| A. | 2 | B. | 4 | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
17.二次根式$\sqrt{1-x}$中,x的取值范围是( )
| A. | x>1 | B. | x≥1 | C. | x<1 | D. | x≤1 |
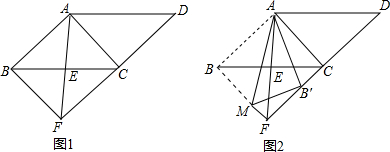
14. 如图,AD∥BC,∠B=30°,DB平分∠ADE,则∠DEC的度数为( )
如图,AD∥BC,∠B=30°,DB平分∠ADE,则∠DEC的度数为( )
 如图,AD∥BC,∠B=30°,DB平分∠ADE,则∠DEC的度数为( )
如图,AD∥BC,∠B=30°,DB平分∠ADE,则∠DEC的度数为( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
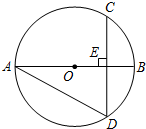 如图,已知在⊙O中,弦CD垂直于直径AB,垂足为点E,如果∠BAD=30°,OE=2,那么CD=4$\sqrt{3}$.
如图,已知在⊙O中,弦CD垂直于直径AB,垂足为点E,如果∠BAD=30°,OE=2,那么CD=4$\sqrt{3}$.