题目内容
20.矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则BC的长是( )| A. | 2 | B. | 4 | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
分析 根据矩形性质得出AO=OC,BO=OD,AC=BD,推出OA=OB,得出△AOB是等边三角形,则可以求得AC的长,然后利用勾股定理求得BC的长.
解答 解:∵四边形ABCD是矩形,
∴AO=OC,BO=OD,AC=BD,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴OA=OB=AB=2,
∴AC=BD=2AO=4,
则BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
故选C.
点评 本题考查了矩形的性质,等边三角形的性质和判定的应用,注意:矩形的对角线相等且互相平分,难度适中.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
8.若点A在第二象限,且到x轴的距离为2,到y轴的距离为3,则点A的坐标为( )
| A. | (-3,2) | B. | (3,-2) | C. | (-2,3) | D. | (2,-3) |
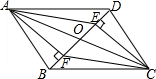 如图,在四边形ABCD中,AB=CD,BE=DF;AE⊥BD,CF⊥BD,对角线AC、BD相交于点O,求证:AO=CO.
如图,在四边形ABCD中,AB=CD,BE=DF;AE⊥BD,CF⊥BD,对角线AC、BD相交于点O,求证:AO=CO.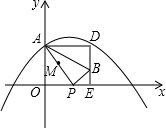 如图,在平面直角坐标系xOy中,抛物线y=ax2+$\frac{5}{6}$x+c过点A(0,4)和C(8,0),P(t,0)是x轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB.过点B作x轴的垂线、过点A作y轴的垂线,两直线相交于点D.
如图,在平面直角坐标系xOy中,抛物线y=ax2+$\frac{5}{6}$x+c过点A(0,4)和C(8,0),P(t,0)是x轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB.过点B作x轴的垂线、过点A作y轴的垂线,两直线相交于点D.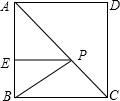 如图,正方形ABCD中,点E在边AB上,且BE=$\sqrt{2}$,AE=3BE,点P在线段AC上的运动,则PE+PB的最小值为5$\sqrt{2}$.
如图,正方形ABCD中,点E在边AB上,且BE=$\sqrt{2}$,AE=3BE,点P在线段AC上的运动,则PE+PB的最小值为5$\sqrt{2}$.