题目内容
7.以下四个命题:①如果三角形一边的中点到其他两边距离相等,那么这个三角形一定是等腰三角形:②两条对角线互相垂直且相等的四边形是正方形:③一组数据2,4,6.4的方差是2;④△OAB与△OCD是以O为位似中心的位似图形,且位似比为1:4,已知∠OCD=90°,OC=CD.点A、C在第一象限.若点D坐标为(2$\sqrt{3}$,0),则点A坐标为($\frac{\sqrt{3}}{4}$,$\frac{\sqrt{3}}{4}$),其中正确命题有①③④(填正确命题的序号即可)分析 ①根据等腰三角形的判定,可得答案;②根据正方形的判定,可得答案;③根据方差的公式,可得答案;④根据相似三角形的性质,可得答案.
解答 解:①如果三角形一边的中点到其他两边距离相等,那么这个三角形一定是等腰三角形,故①正确;
②两条对角线互相垂直且相等的四边形是正方形或等腰梯形,故②错误;
③一组数据2,4,6.4的方差是2,故③正确;
④△OAB与△OCD是以O为位似中心的位似图形,且位似比为1:4,已知∠OCD=90°,OC=CD.
点A、C在第一象限.若点D坐标为(2$\sqrt{3}$,0)得,C($\sqrt{3}$,$\sqrt{3}$).
由位似比为1:4,得
点A坐标为($\frac{\sqrt{3}}{4}$,$\frac{\sqrt{3}}{4}$),故④正确;
故答案为:①③④.
点评 本题考查了命题与定理,利用等腰三角形的判定,正方形的判定是解题关键;注意利用等腰直角三角形的性质的出C点坐标是解题关键,又利用相似比得出A点坐标.

练习册系列答案
相关题目
17.一个三位数,3个数位上的数字和是15,百位上的数字比十位上的数字小1,个位上的数字比十位上的数字大1,则这个三位数是( )
| A. | 345 | B. | 357 | C. | 456 | D. | 567 |
18.下列命题是真命题的是( )
| A. | 若x>y,则x2>y2 | B. | 若|a|=|b|,则a=b | C. | 若a>|b|,则a2>b2 | D. | 若a<1,则a>$\frac{1}{a}$ |
12.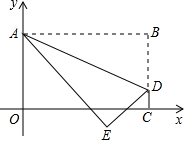 如图,将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C在x轴上,点D(3$\sqrt{5}$,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.若抛物线y=ax2-4$\sqrt{5}$ax+10(a≠0且a为常数)的顶点落在△ADE的内部,则a的取值范围是( )
如图,将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C在x轴上,点D(3$\sqrt{5}$,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.若抛物线y=ax2-4$\sqrt{5}$ax+10(a≠0且a为常数)的顶点落在△ADE的内部,则a的取值范围是( )
 如图,将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C在x轴上,点D(3$\sqrt{5}$,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.若抛物线y=ax2-4$\sqrt{5}$ax+10(a≠0且a为常数)的顶点落在△ADE的内部,则a的取值范围是( )
如图,将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C在x轴上,点D(3$\sqrt{5}$,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.若抛物线y=ax2-4$\sqrt{5}$ax+10(a≠0且a为常数)的顶点落在△ADE的内部,则a的取值范围是( )| A. | $\frac{2}{5}<a<\frac{13}{20}$ | B. | $\frac{2}{5}<a<\frac{11}{20}$ | C. | $\frac{11}{20}<a<\frac{3}{5}$ | D. | $\frac{3}{5}<a<\frac{13}{20}$ |
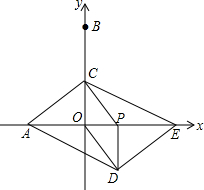 如图,在平面直角坐标系中,点A、B的坐标分别是(-2,0)、(0,4).动点P从O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C以每秒2个单位的速度在y轴上从点B出发运动到点O停止,点C停止运动时点P也随之停止运动.以CP、CO为邻边构造?PCOD,在线段OP的延长线长取点E,使得PE=2.设点P的运动时间为t秒.
如图,在平面直角坐标系中,点A、B的坐标分别是(-2,0)、(0,4).动点P从O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C以每秒2个单位的速度在y轴上从点B出发运动到点O停止,点C停止运动时点P也随之停止运动.以CP、CO为邻边构造?PCOD,在线段OP的延长线长取点E,使得PE=2.设点P的运动时间为t秒.