题目内容
14.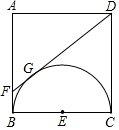 如图,正方形ABCD的边长为4,以BC为直径作半圆E,过点D作DF切半圆E于点G,交AB于点F,则BF的长为1.
如图,正方形ABCD的边长为4,以BC为直径作半圆E,过点D作DF切半圆E于点G,交AB于点F,则BF的长为1.
分析 首先证明DC=DG=4,FB=FG,设FB=FG=x,则有AF=AB-BF=4-x,DF=DG+FG=4+x,在Rt△ADF中,根据DF2=AF2+AD2,列出方程即可解决问题
解答 解:∵AB⊥BC,
∴AB为圆O的切线,
又DF为圆O的切线,
∴DC=DG=4,
同理得到FB=FG,设FB=FG=x,则有AF=AB-BF=4-x,DF=DG+FG=4+x,
在Rt△ADF中,利用勾股定理得:DF2=AF2+AD2,即(4+x)2=42+(4-x)2,
解得:x=1,
∴BF=1,
故答案为1.
点评 此题考查了切线的性质,正方形的性质,等腰三角形的判定与性质,以及勾股定理,熟练掌握切线的性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
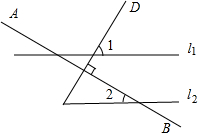 如图,直线l1∥l2,AB⊥CD,∠1=56.5°,那么∠2=33.5°.
如图,直线l1∥l2,AB⊥CD,∠1=56.5°,那么∠2=33.5°.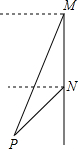 如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为41.682(由科学计算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)
如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为41.682(由科学计算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)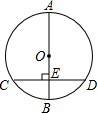 如图,在⊙O中,AB是直径,CD是弦,且AB⊥CD于点E,CD=8,BE=2.求⊙O的半径.
如图,在⊙O中,AB是直径,CD是弦,且AB⊥CD于点E,CD=8,BE=2.求⊙O的半径.