题目内容
9.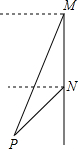 如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为41.682(由科学计算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)
如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为41.682(由科学计算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)
分析 由题意知MN=2×30=60(海里),∠PMN=90°-68°=22°,∠PNA=90°-46°=44°,从而得出∠MPN=∠PMN=22°,即PN=MN=60,依据PA=PNsin∠PNA可得答案.
解答 解:作PA⊥MN,交MN的延长线与A,
由题意知MN=2×30=60(海里),∠PMN=90°-68°=22°,∠PNA=90°-46°=44°,
∴∠MPN=∠PNA-∠PMN=22°,
∴∠MPN=∠PMN,
∴PN=MN=60,
则PA=PNsin∠PNA≈60×0.6947=41.682(海里),
故答案为:41.682.
点评 本题主要考查解直角三角形的应用-仰角俯角问题,在解决有关方向角的问题中,一般要根据题意理清图形中各角的关系,有时所给的方向角并不一定在直角三角形中,需要用到两直线平行内错角相等或一个角的余角等知识转化为所需要的角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.数a增加9.6%后再增加10%的结果是( )
| A. | a(1+9.6%+10%) | B. | a(1+9.6%×10%) | C. | a(1+9.6%)(1+10%) | D. | a(1+9.6%)2(1+10%) |
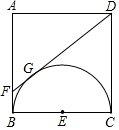 如图,正方形ABCD的边长为4,以BC为直径作半圆E,过点D作DF切半圆E于点G,交AB于点F,则BF的长为1.
如图,正方形ABCD的边长为4,以BC为直径作半圆E,过点D作DF切半圆E于点G,交AB于点F,则BF的长为1. 如图,以△ABC的AB边为直径作⊙O,交BC于点D,过点D作⊙O的切线DE,交AC于点E,且DE⊥AC,连接EO.
如图,以△ABC的AB边为直径作⊙O,交BC于点D,过点D作⊙O的切线DE,交AC于点E,且DE⊥AC,连接EO. 如图,AB=AD,AB⊥AD,AE⊥AC,AE=AC,连接BE,过A作AH⊥CD于H,交BE于F.求证:
如图,AB=AD,AB⊥AD,AE⊥AC,AE=AC,连接BE,过A作AH⊥CD于H,交BE于F.求证: