题目内容
2．若关于x的不等式ax+b＞0的解集为{x|x＜2}，则函数y=ax2-bx+c在x≥-1的范围内单调递减（填“增”或“减”）分析 根据不等式的解集判断出a＜0并求出$\frac{b}{a}$=-2，然后求出二次函数的对称轴，再根据二次函数的增减性解答．
解答 解：∵关于x的不等式ax+b＞0的解集为{x|x＜2}，
∴a＜0且-$\frac{b}{a}$=2，
∴$\frac{b}{a}$=-2，
∴二次函数开口向下，对称轴为直线x=-$\frac{-b}{2a}$=$\frac{b}{2a}$=-1，
∴函数y=ax2-bx+c在x≥-1的范围内单调递减．
故答案为：-1；减．
点评 本题考查了二次函数与不等式，主要利用了二次函数的对称轴以及二次函数的增减性，解题的关键在于根据不等式的解集判断出a是负数并求出a、b的关系．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
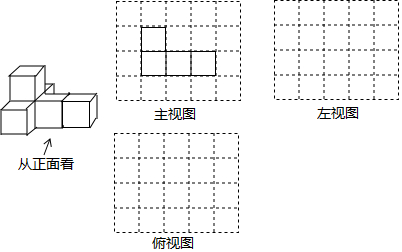
如图1，在正方形ABCD中，E、F分别为DC、BC边上的点，且满足∠EAF=45°，连结EF．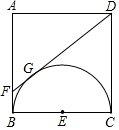
如图，正方形ABCD的边长为4，以BC为直径作半圆E，过点D作DF切半圆E于点G，交AB于点F，则BF的长为1．