题目内容
19.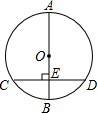 如图,在⊙O中,AB是直径,CD是弦,且AB⊥CD于点E,CD=8,BE=2.求⊙O的半径.
如图,在⊙O中,AB是直径,CD是弦,且AB⊥CD于点E,CD=8,BE=2.求⊙O的半径.
分析 连接OC,根据垂径定理求出CE,根据勾股定理得出方程,求出方程的解即可.
解答 解:连接OC,
设⊙O的半径为x.
∵直径AB⊥弦CD,
∴$CE=\frac{1}{2}CD=4$,
在Rt△OEC中,由勾股定理可得x2=(x-2)2+42,
解得 x=5,
∴⊙O的半径为5.
点评 本题考查了垂径定理和勾股定理,能根据垂径定理求出CE是解此题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
4.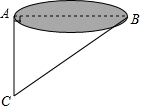 如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.
如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.
 如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.
如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.| A. | 75•sin55° | B. | 75•cos55° | C. | 75•tan55° | D. | $\frac{75}{tan55°}$ |
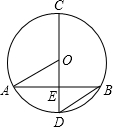 已知:如图,在⊙O中,直径CD交弦AB于点E,且CD平分弦AB,连接OA,BD.
已知:如图,在⊙O中,直径CD交弦AB于点E,且CD平分弦AB,连接OA,BD. 如图1,在正方形ABCD中,E、F分别为DC、BC边上的点,且满足∠EAF=45°,连结EF.
如图1,在正方形ABCD中,E、F分别为DC、BC边上的点,且满足∠EAF=45°,连结EF.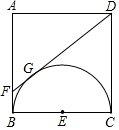 如图,正方形ABCD的边长为4,以BC为直径作半圆E,过点D作DF切半圆E于点G,交AB于点F,则BF的长为1.
如图,正方形ABCD的边长为4,以BC为直径作半圆E,过点D作DF切半圆E于点G,交AB于点F,则BF的长为1.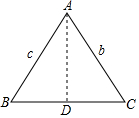 利用三角函数的定义我们可以证明某些结论,已知△ABC中,AB=c,BC=a,CA=b,则有c2=a2+b2-2abcosC,你能证明这个结论吗?(利用如图,作AD⊥BC)
利用三角函数的定义我们可以证明某些结论,已知△ABC中,AB=c,BC=a,CA=b,则有c2=a2+b2-2abcosC,你能证明这个结论吗?(利用如图,作AD⊥BC)