题目内容
16.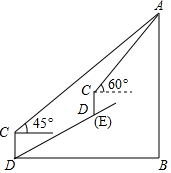 如图,在一次数学课外实践活动中,要求测量山坡前某建筑物的高度 AB.小刚在D处用高1.5m的测角仪CD,测得该建筑物顶端A的仰角为45°,然后沿倾斜角为30°的山坡向上前进20m到达E,重新安装好测角仪CD后又测得该建筑物顶端A的仰角为60°.求该建筑物的高度AB.(结果保留根号)
如图,在一次数学课外实践活动中,要求测量山坡前某建筑物的高度 AB.小刚在D处用高1.5m的测角仪CD,测得该建筑物顶端A的仰角为45°,然后沿倾斜角为30°的山坡向上前进20m到达E,重新安装好测角仪CD后又测得该建筑物顶端A的仰角为60°.求该建筑物的高度AB.(结果保留根号)
分析 作C′M⊥AB于M,MC′的延长线与DC的延长线交于N,作CG⊥AB于G,D′F⊥CD于F,设AM为xm,解Rt△AC′M与Rt△DD′F,用含x的代数式表示出AG、CG,然后根据△ACG是等腰直角三角形得出AG=CG,依此列出方程,解方程即可求出AM,结合图形计算即可.
解答 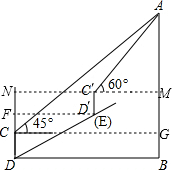 解:如图,作C′M⊥AB于M,MC′的延长线与DC的延长线交于N,作CG⊥AB于G,D′F⊥CD于F,设AM为xm,
解:如图,作C′M⊥AB于M,MC′的延长线与DC的延长线交于N,作CG⊥AB于G,D′F⊥CD于F,设AM为xm,
∵在Rt△AC′M中,∠AC′M=60°,
∴C′M=$\frac{\sqrt{3}}{3}$xm.
∵在Rt△DD′F中,∠DD′F=30°,DD′=20m,
∴DF=$\frac{1}{2}$DD′=10m,D′F=10$\sqrt{3}$m,
∴C′N=D′F=10$\sqrt{3}$m,MN=MC′+C′N=$\frac{\sqrt{3}}{3}$x+10$\sqrt{3}$,
∴CG=MN=$\frac{\sqrt{3}}{3}$x+10$\sqrt{3}$.
∵CN=CF+FN=CF+C′D′=CF+CD=DF=10,
∴AG=AM+MG=AM+CN=x+10.
∵在Rt△ACG中,∠ACG=45°,
∴AG=CG,
∴x+10=$\frac{\sqrt{3}}{3}$x+10$\sqrt{3}$,
解得,x=10$\sqrt{3}$,
则该建筑物的高度AB=AM+MG+GB=AM+CN+CD=10$\sqrt{3}$+10+1.5=10$\sqrt{3}$+11.5.
答:该建筑物的高度AB为(10$\sqrt{3}$+11.5)m.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,理解仰角俯角的概念、熟记锐角三角函数的概念是解题的关键.

练习册系列答案
相关题目
6.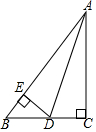 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,则下列结论中正确的是( )
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,则下列结论中正确的是( )
 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,则下列结论中正确的是( )
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,则下列结论中正确的是( )| A. | BD+ED=AC | B. | BD+ED=AD | C. | DE平分∠ADB | D. | ED+AC>AD |
5.某百货商场的某种商品预计在今年平均每月售出100千克,一月份比预计平均月销售量多10千克记为+10千克,以后每月销售量和其前一个月销售量比较,其变化如下表(前11个月):
(1)这11个月中销售量最多的是几月份?最少的是几月份?它们相差多少千克?
(2)前11个月总共销售量是多少?月平均销售量又是多少?
(3)要达到预计的月平均销售量,12月份还需销售多少千克?
| 月 份 | 一月 | 二月 | 三月 | 四月 | 五月 | 六月 | 七月 | 八月 | 九月 | 十月 | 十一月 |
| 销售量变化情况/千克 | +10 | +5 | +1 | +2 | -4 | -4 | -10 | -12 | +5 | +4 | +5.8 |
(2)前11个月总共销售量是多少?月平均销售量又是多少?
(3)要达到预计的月平均销售量,12月份还需销售多少千克?

 已知:如图,PM=PN,∠M=∠N.求证:AM=BN.
已知:如图,PM=PN,∠M=∠N.求证:AM=BN.