题目内容

8．某校九年级数学兴趣小组为了测得该校地下停车场的限高CD，在课外活动时间测得下列数据：如图，从地面E点测得地下停车场的俯角为30°，斜坡AE的长为16米，地面B点（与E点在同一个水平线）距停车场顶部C点（A、C、B在同一条直线上且与水平线垂直）1.2米．试求该校地下停车场的高度AC及限高CD（结果精确到0.1米）．

分析 根据题意和正弦的定义求出AB的长，根据余弦的定义求出CD的长．

解答 解：由题意得，AB⊥EB，CD⊥AE，
∴∠CDA=∠EBA=90°，
∵∠E=30°，
∴AB=$\frac{1}{2}$AE=8米，
∵BC=1.2米，
∴AC=AB-BC=6.8米，
∵∠DCA=90°-∠A=30°，
∴CD=AC×cos∠DCA=6.8×$\frac{\sqrt{3}}{2}$≈5.9米．
答：该校地下停车场的高度AC为6.8米，限高CD约为5.9米．

点评 本题考查的是解直角三角形的应用-仰角俯角问题，理解仰角的概念、灵活运用锐角三角函数的定义是解题的关键．

练习册系列答案
相关题目
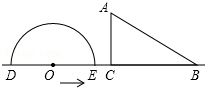18．如图，半圆O直径DE=12，Rt△ABC中，BC=12，∠ACB=90°，∠ABC=30°．半圆O从左到右运动，在运动过程中，点D，E始终在直线BC上，半圆O在△ABC的左侧．
（1）当△ABC的一边与半圆O相切时，请画出符合题意得图形．
（2）当△ABC的一边与半圆O相切时，如果半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分，求重叠部分的面积．
19．若y=（1+m）${x}^{{m}^{2}-7}$是二次函数，且开口向下，则m的值为（　　）
A．±3B．-3C．+3D．0
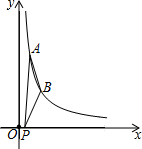16．如图，双曲线$y=\frac{k}{x}$（x＞0）经过点A（1，6）、点B（2，n），点P的坐标为（t，0），且-1≤t＜3，则△PAB的最大面积为6．
3．下面是按一定规律排列的一列数：
第1个数：1-（1+$\frac{-1}{2}$）
第2个数：2-（1+$\frac{-1}{2}$）[1+$\frac{（-1）^{2}}{3}$][1+$\frac{（-1）^{3}}{4}$]
第3个数：3-（1+$\frac{-1}{2}$）[1+$\frac{（-1）^{2}}{3}$][1+$\frac{（-1）^{3}}{4}$][1+$\frac{（-1）^{4}}{5}$][1+$\frac{（-1）^{5}}{6}$]
…
（1）填空：
第1个数的计算结果是$\frac{1}{2}$，第2个数的计算结果是$\frac{3}{2}$，第3个数的计算结果是$\frac{5}{2}$；
（2）写出第2015个数的形式，要求中间部分用省略号，两端部分写详细；
2015-（1+$\frac{-1}{2}$）[1+$\frac{（-1）^{2}}{3}$][1+$\frac{（-1）^{3}}{4}$]…[1+$\frac{（-1）^{4028}}{4029}$][1+$\frac{（-1）^{4029}}{4030}$]
（3）根据之前的推算，第2015个算式的结果是$\frac{4029}{2}$．
13．已知，在菱形ABCD中，∠ADC=60°，点H为CD上任意一点（不与C、D重合），过点H作CD的垂线，交BD于点E，连接AE．
（1）如图1，线段EH、CH、AE之间的数量关系是EH2+CH2=AE2；
（2）如图2，将△DHE绕点D顺时针旋转，当点E、H、C在一条直线上时，求证：AE+EH=CH．
20．先化简，再求值：$\frac{3-x}{x-2}÷$（x+2-$\frac{5}{x-2}$），其中x=$\frac{2}{3}$．
17．如图，在Rt△ABC中，∠A=90°，D是BC的中点，DE⊥BC，垂足为D，交AB于点E，连接CE，若AE=3，BE=5，则边AC的长为（　　）
A．3B．4C．6D．8
18．如图，在Rt△ABC中，∠C=90°，BC=3，AC=4，则sinA的值是（　　）
A．$\frac{3}{4}$B．$\frac{4}{3}$C．$\frac{3}{5}$D．$\frac{4}{5}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网