题目内容
如图，点A、B、C在⊙O上，∠ABO=30°，∠ACO=45°，则∠BOC等于（ ）| A、60° | B、90° |
| C、150° | D、160° |
考点：圆周角定理
专题：
分析：过A、O作⊙O的直径AD，分别在等腰△OAB、等腰△OAC中，根据三角形外角的性质求出∠BOC=2∠ABO+2∠ACO．
解答：
解：过A作⊙O的直径，交⊙O于D；
在△OAB中，OA=OB，
则∠BOD=∠ABO+∠OAB=2×30°=60°，
同理可得：∠COD=∠ACO+∠OAC=2×45°=90°，
故∠BOC=∠BOD+∠COD=150°．
故选C．
解：过A作⊙O的直径，交⊙O于D；在△OAB中，OA=OB，
则∠BOD=∠ABO+∠OAB=2×30°=60°，
同理可得：∠COD=∠ACO+∠OAC=2×45°=90°，
故∠BOC=∠BOD+∠COD=150°．
故选C．
点评：本题考查了圆周角定理，涉及了等腰三角形的性质及三角形的外角性质，解答本题的关键是求出∠COD及∠BOD的度数．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
将?ABCD绕O点旋转到?A′B′C′D′的位置，错误的是（ ）
| A、AB=A′B′ |
| B、AB一定平行于A′B′ |
| C、∠B=∠B′ |
| D、△ABC≌△A′B′C′ |
如果两个角的差的绝对值等于90°，就称这两个角互为反余角，其中一个角叫做另一个角的反余角．例如：∠1=120°，∠2=30°，∠1-∠2=90°，则∠1和∠2互为反余角，其中∠1是∠2的反余角，∠2也是∠1的反余角．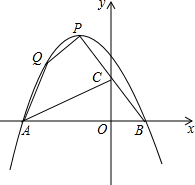
已知抛物线y=ax2-x+c经过点Q（-1，2），且它的顶点P的横坐标为-1．设抛物线与x轴相交于A、B两点，
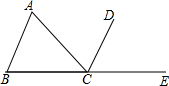如图所示，在△ABC中，以C为顶点，在△ABC外作∠ACD=∠A，且点A和点D在直线BC的同侧，延长BC至E，在所作的图形中：
如图，OC⊥AB于O，若∠AOD：∠COD=2：7，∠BOE：∠AOE=2：3，求∠DOE的度数．
如图，在?ABCD中，E，F为BD上的点，BF=DE，那么四边形AECF是什么图形？试用两种方法证明．