题目内容
 如图,OC⊥AB于O,若∠AOD:∠COD=2:7,∠BOE:∠AOE=2:3,求∠DOE的度数.
如图,OC⊥AB于O,若∠AOD:∠COD=2:7,∠BOE:∠AOE=2:3,求∠DOE的度数.考点:垂线
专题:
分析:根据垂线的定义,可得∠AOC的度数,根据∠AOD:∠COD=2:7,可得∠AOD,根据∠BOE:∠AOE=2:3,可得∠AOE,再根据角的和差,可得答案.
解答:解:由OC⊥AB于O,得∠AOC=90°,
由∠AOD:∠COD=2:7,得
∠AOD=90°×
=20°,
由∠BOE:∠AOE=2:3,得
∠AOE=180°×
=108°,
由角的和差,得
∠DOE=∠AOE-∠AOD=108°-20°=88°.
由∠AOD:∠COD=2:7,得
∠AOD=90°×
| 2 |
| 2+7 |
由∠BOE:∠AOE=2:3,得
∠AOE=180°×
| 3 |
| 2+3 |
由角的和差,得
∠DOE=∠AOE-∠AOD=108°-20°=88°.
点评:本题考查了垂线,利用了垂线的定义,按比例分配,角的和差.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,有两个相似的星星图案,则x的值为( )
如图,有两个相似的星星图案,则x的值为( )| A、8 | B、10 | C、12 | D、15 |
 如图,点A、B、C在⊙O上,∠ABO=30°,∠ACO=45°,则∠BOC等于( )
如图,点A、B、C在⊙O上,∠ABO=30°,∠ACO=45°,则∠BOC等于( )| A、60° | B、90° |
| C、150° | D、160° |
下列说法错误的是( )
| A、长方体、正方体都是棱柱 |
| B、六棱柱有六条棱、六个侧面 |
| C、三棱柱的侧面是三角形 |
| D、球体的三种视图均为同样的图形 |
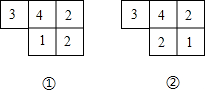 如图都是由几个小正方体所搭成的几何体的俯视图,小正方体中的数字表示在该位置的小正方体的个数.
如图都是由几个小正方体所搭成的几何体的俯视图,小正方体中的数字表示在该位置的小正方体的个数. 如图,直线AB,CD相交于点O,根据图示条件,求出x.
如图,直线AB,CD相交于点O,根据图示条件,求出x. 如图,等腰直角三角形ABC斜边AB为2
如图,等腰直角三角形ABC斜边AB为2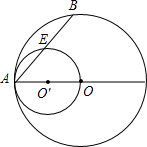 如图,⊙O的半径OA=2cm,以OA为直径的⊙O′交⊙O的弦AB于点E,若BE=
如图,⊙O的半径OA=2cm,以OA为直径的⊙O′交⊙O的弦AB于点E,若BE=