题目内容
15. 如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D.如果∠ABC=60°,BC=9,那么AE等于( )
如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D.如果∠ABC=60°,BC=9,那么AE等于( )| A. | 6 | B. | 6$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 9 |
分析 根据正切的概念求出EC,根据角平分线的性质求出DE,根据直角三角形的性质计算即可.
解答 解:∵BE平分∠ABC,∠ABC=60°,
∴∠CBE=30°,
∴EC=BC×tan∠CBE=3$\sqrt{3}$,
∵BE平分∠ABC,∠ACB=90°,ED⊥AB,
∴DE=EC=3$\sqrt{3}$,
∠ACB=90°,∠ABC=60°,
∴∠A=30°,
∴AE=2DE=6$\sqrt{3}$,
故选:B.
点评 本题考查的是直角三角形的性质、角平分线的性质,掌握直角三角形中,30°角所对的直角边等于斜边的一半是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
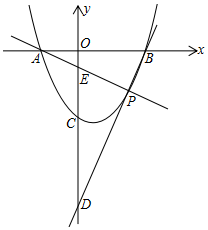 如图,已知抛物线y=x2-(2m+1)x+m2+m-2与x轴交于A、B两点,点A在点B的左边,与y轴交于点C,P(s,t)为抛物线上A、B之间一点(不包括A、B),连接AP、BP分别交y轴于点E、D
如图,已知抛物线y=x2-(2m+1)x+m2+m-2与x轴交于A、B两点,点A在点B的左边,与y轴交于点C,P(s,t)为抛物线上A、B之间一点(不包括A、B),连接AP、BP分别交y轴于点E、D
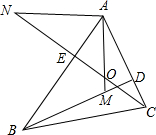 如图,在△ABC中,CE,BD为高线,M、N在BD,CE(或延长线上),且BM=AC,CN=AB.
如图,在△ABC中,CE,BD为高线,M、N在BD,CE(或延长线上),且BM=AC,CN=AB.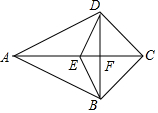 如图,在四边形ABCD中,AC与BD相交于点F,E为AC上一点,且AD=AB,ED=EB.
如图,在四边形ABCD中,AC与BD相交于点F,E为AC上一点,且AD=AB,ED=EB.