题目内容
5.在平面直角坐标系中,已知点P0的坐标为(1,0),将P0绕原点O按逆时针方向旋转30°得点P1,延长OP1到P2,使OP2=2OP1,再将点P2绕原点O按逆时针方向转动30°得到点P3,延长OP3到P4,使OP4=2OP3,…,如果继续下去,点P2016的坐标为(21008,0).分析 根据每次旋转后线段的长度是原来的2倍求出OP2016,根据旋转角为30°求出每12次旋转,24个点为一个循环组依次循环,然后用2016除以24,再根据商和余数的情况确定出点P2016的在x轴正半轴,然后解答即可.
解答 解:∵点P0的坐标为(1,0),
∴OP0=1,
∴OP2=2OP1=2,
OP3=OP2=2,
OP4=2OP3=2×2=22,
…,
OP2016=21008,
∵2016÷24=84,
∴点P2016是第84循环组的最后一个点,在x轴正半轴,
∴点P2016的坐标为(21008,0).
故答案为:(21008,0).
点评 本题考查了坐标与图形变化-旋转,点的坐标的变化规律,读懂题目信息,理解点的规律变化是解题的关键.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
3.在-4、-2、0、1、3、4这六个数中,正数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.二次函数y=(x-m)2-m2-1有最小值-4,则实数m的值可能是( )
| A. | -$\sqrt{3}$ | B. | -3 | C. | $\sqrt{5}$ | D. | 4 |
20.在△ABC中,∠C=90°,tanA=1,那么cosB等于( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{\sqrt{2}}{2}$ |
10.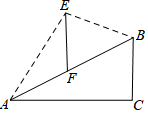 如图,小明家附近有一斜坡AB=40米,其坡度$i=1:\sqrt{3}$,斜坡AB上有一竖直向上的古树EF,小明在山底A处看古树树顶E的仰角为60°,在山顶B处看古树树顶E的仰角为15°,则古树的高约为(参考数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$)( )
如图,小明家附近有一斜坡AB=40米,其坡度$i=1:\sqrt{3}$,斜坡AB上有一竖直向上的古树EF,小明在山底A处看古树树顶E的仰角为60°,在山顶B处看古树树顶E的仰角为15°,则古树的高约为(参考数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$)( )
 如图,小明家附近有一斜坡AB=40米,其坡度$i=1:\sqrt{3}$,斜坡AB上有一竖直向上的古树EF,小明在山底A处看古树树顶E的仰角为60°,在山顶B处看古树树顶E的仰角为15°,则古树的高约为(参考数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$)( )
如图,小明家附近有一斜坡AB=40米,其坡度$i=1:\sqrt{3}$,斜坡AB上有一竖直向上的古树EF,小明在山底A处看古树树顶E的仰角为60°,在山顶B处看古树树顶E的仰角为15°,则古树的高约为(参考数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$)( )| A. | 16.9 米 | B. | 13.7米 | C. | 14.6米 | D. | 15.2米 |
15. 如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D.如果∠ABC=60°,BC=9,那么AE等于( )
如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D.如果∠ABC=60°,BC=9,那么AE等于( )
 如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D.如果∠ABC=60°,BC=9,那么AE等于( )
如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D.如果∠ABC=60°,BC=9,那么AE等于( )| A. | 6 | B. | 6$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 9 |
 如图,线段AB=2n,点P是线段AD上的动点(不包括端点),分别以AP.BP为斜边,在线段AB两侧作等腰Rt△ACP和等腰Rt△BDP,则C、D两点之间的距离为$\sqrt{2}$n.(用含n的代数式表示)
如图,线段AB=2n,点P是线段AD上的动点(不包括端点),分别以AP.BP为斜边,在线段AB两侧作等腰Rt△ACP和等腰Rt△BDP,则C、D两点之间的距离为$\sqrt{2}$n.(用含n的代数式表示)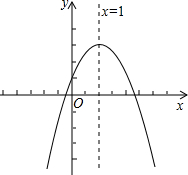 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论: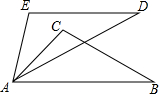 如图,AE=AC,∠E=∠C=80°,ED=CB,∠D=40°,∠CAD=35°,则∠BAE的度数是85°.
如图,AE=AC,∠E=∠C=80°,ED=CB,∠D=40°,∠CAD=35°,则∠BAE的度数是85°.