题目内容
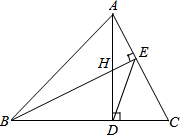 如图,△ABC的高AD、BE交于点H,若BH=AC,证明:
如图,△ABC的高AD、BE交于点H,若BH=AC,证明:(1)∠ABC=45°;
(2)DH=DC;
(3)∠CED=45°.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)求出∠ADC=∠BDH=90°,∠CAD=∠DBH,根据AAS推出△ADC≌△BDH,根据等腰三角形性质和三角形的内角和定理求出即可;
(2)根据全等三角形的性质得出即可;
(3)证A、B、D、E四点共圆,根据圆内接四边形的性质得出即可.
(2)根据全等三角形的性质得出即可;
(3)证A、B、D、E四点共圆,根据圆内接四边形的性质得出即可.
解答:证明:(1)∵△ABC的高AD、BE交于点H,
∴∠BEC=∠ADC=∠BDH=90°,
∴∠DBH+∠C=90°,∠DAC+∠C=90°,
∴∠DBH=∠DAC,
在△ADC和△BDH中,
,
∴△ADC≌△BDH(AAS),
∴AD=BD,
∵∠ADB=90°,
∴∠ABC=∠BAD=45°;
(2)∵△ADC≌△BDH,
∴DH=DC;
(3)∵∠AEB=∠ADB=90°,
∴A、B、D、E四点共圆,
∴∠CED=∠ABC=45°.
∴∠BEC=∠ADC=∠BDH=90°,
∴∠DBH+∠C=90°,∠DAC+∠C=90°,
∴∠DBH=∠DAC,
在△ADC和△BDH中,
|
∴△ADC≌△BDH(AAS),
∴AD=BD,
∵∠ADB=90°,
∴∠ABC=∠BAD=45°;
(2)∵△ADC≌△BDH,
∴DH=DC;
(3)∵∠AEB=∠ADB=90°,
∴A、B、D、E四点共圆,
∴∠CED=∠ABC=45°.
点评:本题考查了等腰三角形的性质,全等三角形的性质和判定,三角形的内角和定理,圆内接四边形的性质的应用,主要考查学生的推理能力,难度偏大.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目

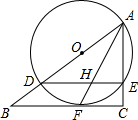 如图,在Rt△ABC中,∠C=90°,点D是AB上一点,以AD为直径作⊙O交AC于E,与BC相切于点F,连接AF.
如图,在Rt△ABC中,∠C=90°,点D是AB上一点,以AD为直径作⊙O交AC于E,与BC相切于点F,连接AF.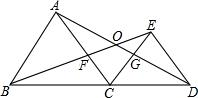 如图△DCE、△ABC均为等边三角形,AD、BE分别交与CE、AC交于点G、F,有下列结论:
如图△DCE、△ABC均为等边三角形,AD、BE分别交与CE、AC交于点G、F,有下列结论: 如图,在?ABCD中,BC=2CD,点M、N分别在BC、CD边上,AM与BN交于点E.若∠C=∠AEN,BN=5
如图,在?ABCD中,BC=2CD,点M、N分别在BC、CD边上,AM与BN交于点E.若∠C=∠AEN,BN=5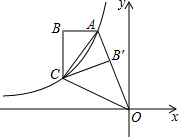 如图,双曲线y=
如图,双曲线y= 如图,AB是⊙O的直径,
如图,AB是⊙O的直径,