题目内容
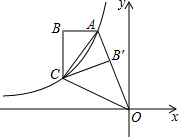 如图,双曲线y=
如图,双曲线y=| k |
| x |
考点:反比例函数综合题
专题:计算题
分析:延长BC,与x轴交于点D,可得CD⊥x轴,作AE⊥x轴,如图所示,由折叠的性质得到Rt△ABC≌Rt△AB′C,再由角平分线定理得到BC=B′C=CD=b,AB=m,设A(-a,2b),根据题意求出mb=4,2ab=k,利用反比例函数的性质列出关于k的方程,求出方程的解即可得到k的值.
解答: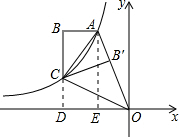 解:延长BC,与x轴交于点D,可得CD⊥x轴,作AE⊥x轴,如图所示,
解:延长BC,与x轴交于点D,可得CD⊥x轴,作AE⊥x轴,如图所示,
∵Rt△ABC沿AC翻折后得到Rt△AB′C,且Rt△ABC的面积为2,
∴Rt△ABC≌Rt△AB′C,
∵OC平分∠AOD,CD⊥OD,CB′⊥OA,
∴CD=CB′=CB,
设AB=m,A(a,2b),BC=b,则OD=m-a,
bm=2,即bm=4,
∴S△COD=-
k=
OD•CD=
(m-a)b=
(mb-ab)=
(4-
)=2-
,
解得:k=-8.
故答案为:-8.
 解:延长BC,与x轴交于点D,可得CD⊥x轴,作AE⊥x轴,如图所示,
解:延长BC,与x轴交于点D,可得CD⊥x轴,作AE⊥x轴,如图所示,∵Rt△ABC沿AC翻折后得到Rt△AB′C,且Rt△ABC的面积为2,
∴Rt△ABC≌Rt△AB′C,
∵OC平分∠AOD,CD⊥OD,CB′⊥OA,
∴CD=CB′=CB,
设AB=m,A(a,2b),BC=b,则OD=m-a,
| 1 |
| 2 |
∴S△COD=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| 2 |
| k |
| 4 |
解得:k=-8.
故答案为:-8.
点评:此题属于反比例函数综合题,涉及的知识有:折叠的性质,角平分线定理,以及反比例函数的性质,熟练掌握反比例函数的性质是解本题的关键.

练习册系列答案
相关题目
 如图,△ABC中,D为BC上的一点,且S△ACD=S△ABD,则AD为( )
如图,△ABC中,D为BC上的一点,且S△ACD=S△ABD,则AD为( )| A、高 | B、中线 |
| C、角平分线 | D、不能确定 |
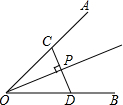 如图,P是∠AOB平分线上一点,CD⊥OP于F,并分别交OA、OB于CD,则CD( )P点到∠AOB两边距离之和.
如图,P是∠AOB平分线上一点,CD⊥OP于F,并分别交OA、OB于CD,则CD( )P点到∠AOB两边距离之和.| A、小于 | B、大于 |
| C、等于 | D、不能确定 |
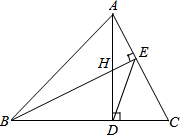 如图,△ABC的高AD、BE交于点H,若BH=AC,证明:
如图,△ABC的高AD、BE交于点H,若BH=AC,证明: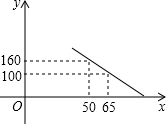 大学生王强积极响应“自主创业”的号召,准备投资销售一种进价为每件40元的小家电.通过试销发现,当销售单价在40元至90元之间(含40元和90元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.求y与x的函数表达式.
大学生王强积极响应“自主创业”的号召,准备投资销售一种进价为每件40元的小家电.通过试销发现,当销售单价在40元至90元之间(含40元和90元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.求y与x的函数表达式.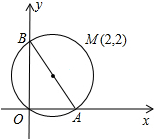 如图,过O和M(2,2)的⊙I,交坐标轴于A、B两点.
如图,过O和M(2,2)的⊙I,交坐标轴于A、B两点.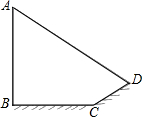 如图,小明想测量一棵大树AB的高度,发现大树的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4m,BC=10m,CD与地面成45°,且此时测得1m竖杆的影子长是2m,求大树的高度是多少米?
如图,小明想测量一棵大树AB的高度,发现大树的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4m,BC=10m,CD与地面成45°,且此时测得1m竖杆的影子长是2m,求大树的高度是多少米? 如图,已知Rt△ABC中,BC=9,AB=12,过点A作AE⊥AB,且AE=16,连接BE交AC于点P.
如图,已知Rt△ABC中,BC=9,AB=12,过点A作AE⊥AB,且AE=16,连接BE交AC于点P.