题目内容
 如图,在?ABCD中,BC=2CD,点M、N分别在BC、CD边上,AM与BN交于点E.若∠C=∠AEN,BN=5
如图,在?ABCD中,BC=2CD,点M、N分别在BC、CD边上,AM与BN交于点E.若∠C=∠AEN,BN=5| 5 |
考点:相似三角形的判定与性质,平行四边形的性质
专题:
分析:易证△ABM∽△AEB和△BEM∽△BCN根据相似三角形对应边比例等于相似比即可求得AM的值.
解答:解:∵∠C=∠AEM,
∴∠AEB=∠ABM(∠ABM+∠C=180°),
∴△ABM∽△AEB,
∴AM:AB=BM:BE,∠ABN=∠AMB,①
∵∠CNB=∠ABN=∠AMB,
∴△BEM∽△BCN
∴NB:BM=BC:BE,②
由①②得:AM:AB=BN:BC,
∴AM=
∵2AB=BC,
∴AM=
=
.
∴∠AEB=∠ABM(∠ABM+∠C=180°),
∴△ABM∽△AEB,
∴AM:AB=BM:BE,∠ABN=∠AMB,①
∵∠CNB=∠ABN=∠AMB,
∴△BEM∽△BCN
∴NB:BM=BC:BE,②
由①②得:AM:AB=BN:BC,
∴AM=
| AB•BN |
| BC |
∵2AB=BC,
∴AM=
| BN |
| 2 |
5
| ||
| 2 |
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比例等于相似比的性质.

练习册系列答案
相关题目
我们知道:
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52.根据前面各式规律,可以猜测:
1+3+5+7+9+…+(2n-1)= .(其中n为自然数).
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52.根据前面各式规律,可以猜测:
1+3+5+7+9+…+(2n-1)=
 如图,△ABC中,D为BC上的一点,且S△ACD=S△ABD,则AD为( )
如图,△ABC中,D为BC上的一点,且S△ACD=S△ABD,则AD为( )| A、高 | B、中线 |
| C、角平分线 | D、不能确定 |

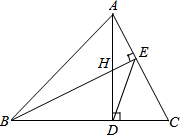 如图,△ABC的高AD、BE交于点H,若BH=AC,证明:
如图,△ABC的高AD、BE交于点H,若BH=AC,证明: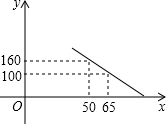 大学生王强积极响应“自主创业”的号召,准备投资销售一种进价为每件40元的小家电.通过试销发现,当销售单价在40元至90元之间(含40元和90元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.求y与x的函数表达式.
大学生王强积极响应“自主创业”的号召,准备投资销售一种进价为每件40元的小家电.通过试销发现,当销售单价在40元至90元之间(含40元和90元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.求y与x的函数表达式.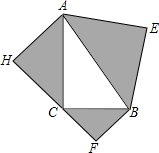 如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形,若斜边AB=a,则图中阴影部分的面积为
如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形,若斜边AB=a,则图中阴影部分的面积为