题目内容
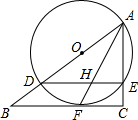如图，在Rt△ABC中，∠C=90°，点D是AB上一点，以AD为直径作⊙O交AC于E，与BC相切于点F，连接AF．（1）求证：∠BAF=∠CAF；
（2）若AC=6，BC=8，求BD和CE的长；
（3）在（2）的条件下，若AF与DE交于H，求FH•FA的值．（直接写出结果即可）
考点：切线的性质
专题：证明题
分析：（1）连结OF，如图，根据切线的性质得OF⊥BC，则易得OF∥AC，所以∠OFA=∠CAF，加上∠OAF=∠OFA，则∠BAF=∠CAF；
（2）设⊙O的半径为r，OF与DE交于点P，如图，在Rt△ABC中根据勾股定理计算出AB=10，再证明△BOF∽△BAC，利用相似比计算出r=
，则BD=BA-AD=
；接着根据圆周角定理由AD为⊙O的直径得到∠AED=90°，易得DE∥BC，根据平行线分线段成比例定理可计算出CE=
；
（3）根据平行线分线段成比例定理，由OF∥AC，
=
，则可计算出CF=3，再在Rt△ACF中，利用勾股定理计算出AF=3
，然后利用HE∥CF得到
=
，可计算出FH=
，最后计算FH•FA的值．
（2）设⊙O的半径为r，OF与DE交于点P，如图，在Rt△ABC中根据勾股定理计算出AB=10，再证明△BOF∽△BAC，利用相似比计算出r=
| 15 |
| 4 |
| 5 |
| 2 |
| 3 |
| 2 |
（3）根据平行线分线段成比例定理，由OF∥AC，
| CF |
| CB |
| AO |
| AB |
| 5 |
| FH |
| FA |
| CE |
| CA |
3
| ||
| 2 |
解答：（1）证明：连结OF，如图，
∵⊙O与BC相切于点F，
∴OF⊥BC，
∵∠ACB=90°，
∴OF∥AC，
∴∠OFA=∠CAF，
而OA=OF，
∴∠OAF=∠OFA，
∴∠BAF=∠CAF；
（2）解：设⊙O的半径为r，OF与DE交于点P，如图，
在Rt△ABC中，∵AC=6，BC=8，
∴AB=
=10，
∵OF∥AC，
∴△BOF∽△BAC，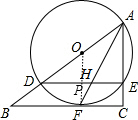
∴
=
，即
=
，解得r=
，
∴BD=BA-AD=10-2×
=
，
∵AD为⊙O的直径，
∴∠AED=90°，
而∠C=90°，
∴DE∥BC，
∴
=
，即
=
，
∴CE=
；
（3）解：∵OF∥AC，
∴
=
，即
=
，解得CF=3，
在Rt△ACF中，AF=
=3
，
∵HE∥CF，
∴
=
，即
=
，
∴FH=
，
∴FH•FA=
•3
=
．
∵⊙O与BC相切于点F，
∴OF⊥BC，
∵∠ACB=90°，
∴OF∥AC，
∴∠OFA=∠CAF，
而OA=OF，
∴∠OAF=∠OFA，
∴∠BAF=∠CAF；
（2）解：设⊙O的半径为r，OF与DE交于点P，如图，
在Rt△ABC中，∵AC=6，BC=8，
∴AB=
| AC2+BC2 |
∵OF∥AC，
∴△BOF∽△BAC，
∴
| OF |
| AC |
| BO |
| BA |
| r |
| 6 |
| 10-r |
| 10 |
| 15 |
| 4 |
∴BD=BA-AD=10-2×
| 15 |
| 4 |
| 5 |
| 2 |
∵AD为⊙O的直径，
∴∠AED=90°，
而∠C=90°，
∴DE∥BC，
∴
| BD |
| BA |
| CE |
| CA |
| ||
| 10 |
| CE |
| 6 |
∴CE=
| 3 |
| 2 |
（3）解：∵OF∥AC，
∴
| CF |
| CB |
| AO |
| AB |
| CF |
| 8 |
| ||
| 10 |
在Rt△ACF中，AF=
| AC2+CF2 |
| 5 |
∵HE∥CF，
∴
| FH |
| FA |
| CE |
| CA |
| FH | ||
3
|
| 3 |
| 6 |
∴FH=
3
| ||
| 2 |
∴FH•FA=
3
| ||
| 2 |
| 5 |
| 45 |
| 2 |
点评：本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了圆周角定平行线分线段成比例定理和勾股定理．
练习册系列答案
相关题目
如图，有一长方形纸片ABCD，将纸片折叠，使点B与点D重合，请画出折痕EF．
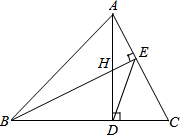如图，△ABC的高AD、BE交于点H，若BH=AC，证明：
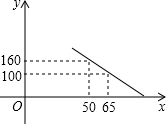大学生王强积极响应“自主创业”的号召，准备投资销售一种进价为每件40元的小家电．通过试销发现，当销售单价在40元至90元之间（含40元和90元）时，每月的销售量y（件）与销售单价x（元）之间的关系可近似地看作一次函数，其图象如图所示．求y与x的函数表达式．
如图，已知Rt△ABC中，BC=9，AB=12，过点A作AE⊥AB，且AE=16，连接BE交AC于点P．