题目内容
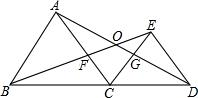 如图△DCE、△ABC均为等边三角形,AD、BE分别交与CE、AC交于点G、F,有下列结论:
如图△DCE、△ABC均为等边三角形,AD、BE分别交与CE、AC交于点G、F,有下列结论:(1)△ACD≌△BCE;(2)CF=CG;(3)CD=EF
其中正确的是
考点:全等三角形的判定与性质,等边三角形的性质
专题:常规题型
分析:(1)先证明∠ACD=∠BCE,即可证明△ACD≌△BCE;
(2)根据旋转的性质可得CF=CG;
(3)证明∠FCG≠∠CFE得出EF≠CE即可.
(2)根据旋转的性质可得CF=CG;
(3)证明∠FCG≠∠CFE得出EF≠CE即可.
解答:解:(1)∵∠ACB=∠ECD,
∴∠BCE=∠DCA,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS);
(2)如图,
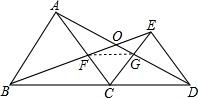
∵△ACD≌△BCE,且∠BCA=∠ACE=∠ECD,
∴可以认为△ACD是△BCE沿C点顺时针旋转60°而来,
∴CF=CG.
(3)∵CF=CG,∠FCG=60°,
∴∠FCG=∠CFG=60°,
∴∠FCG≠∠CFE,
∴EF≠CE,
∵CE=CD,
∴EF≠CD.
故答案为(1)(2).
∴∠BCE=∠DCA,
在△ACD和△BCE中,
|
∴△ACD≌△BCE(SAS);
(2)如图,

∵△ACD≌△BCE,且∠BCA=∠ACE=∠ECD,
∴可以认为△ACD是△BCE沿C点顺时针旋转60°而来,
∴CF=CG.
(3)∵CF=CG,∠FCG=60°,
∴∠FCG=∠CFG=60°,
∴∠FCG≠∠CFE,
∴EF≠CE,
∵CE=CD,
∴EF≠CD.
故答案为(1)(2).
点评:本题考查了全等三角形的判定,考查了旋转的性质,本题中求证△ACD≌△BCE是解题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 如图,有一长方形纸片ABCD,将纸片折叠,使点B与点D重合,请画出折痕EF.
如图,有一长方形纸片ABCD,将纸片折叠,使点B与点D重合,请画出折痕EF.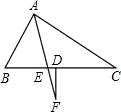 如图,AF平分∠BAC,FD⊥BD.
如图,AF平分∠BAC,FD⊥BD.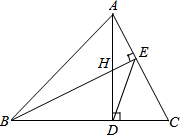 如图,△ABC的高AD、BE交于点H,若BH=AC,证明:
如图,△ABC的高AD、BE交于点H,若BH=AC,证明: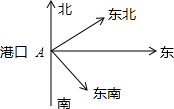 如图,一轮船以16n mi1e/h的速度从港口A出发向东北方向航行,另一轮船以12n mi1e/h的速度同时从港口出发向东南方向航行,那么离开港口A2h后,两船相距多远?
如图,一轮船以16n mi1e/h的速度从港口A出发向东北方向航行,另一轮船以12n mi1e/h的速度同时从港口出发向东南方向航行,那么离开港口A2h后,两船相距多远?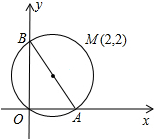 如图,过O和M(2,2)的⊙I,交坐标轴于A、B两点.
如图,过O和M(2,2)的⊙I,交坐标轴于A、B两点.