题目内容
20.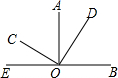 如图,已知AO⊥OB,CO⊥DO,∠BOC=β°,则∠AOD的度数为( )
如图,已知AO⊥OB,CO⊥DO,∠BOC=β°,则∠AOD的度数为( )| A. | β°-90° | B. | 2β°-90° | C. | 180°-β° | D. | 2β°-180° |
分析 首先根据垂直定义可得∠COD=90°,∠AOB=90°,再根据同角的余角相等可得∠BOD=∠AOC,再由条件∠BOC=β,可表示出∠BOD=∠AOC的度数,进而得到答案.
解答 解:∵AO⊥BE,CO⊥DO,
∴∠COD=90°,∠AOB=90°,
即:∠AOD+∠BOD=∠AOD+∠AOC=90°,
∴∠BOD=∠AOC,
∵∠BOC=β°,
∴∠BOD=∠AOC=(β-90)°,
∴∠AOD=90°-β°+90°=180°-β°.
故选:C.
点评 此题主要考查了余角和补角,关键是掌握余角:如果两个角的和等于90°(直角),就说这两个角互为余角.即其中一个角是另一个角的余角.补角:如果两个角的和等于180°(平角),就说这两个角互为补角.即其中一个角是另一个角的补角.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
12.根据下表回答下列问题:
(1)(6×10)3=63×103.(6×0.1)3=63×($\frac{1}{10}$)3.
(2)12.167的立方根是2.3.
(3)$\root{3}{-9.261}$=-2.1.
| x | 0.6 | 6 | 60 | 2 | 2.1 | 2.2 | 2.3 | 2.4 |
| x3 | 0.216 | 216 | 216000 | 8 | 9.261 | 10.648 | 12.167 | 13.824 |
(2)12.167的立方根是2.3.
(3)$\root{3}{-9.261}$=-2.1.
9.利用基本的尺规作图不能作出等腰三角形的是( )
| A. | 已知底边及底边上的高 | B. | 已知底边的上的高及腰 | ||
| C. | 已知底边及顶角 | D. | 已知两底角 |
10.分式$\frac{2c}{3{a}^{2}{b}^{2}}$,$\frac{3a}{-4{b}^{4}c}$,$\frac{5b}{2{a}^{2}c}$的最简公分母是( )
| A. | 12a2b4c2 | B. | 24a2b4c2 | C. | 24a4b6c | D. | 12a2b4c |
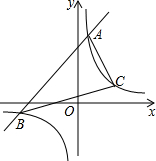 如图,已知直线y1=x+b与双曲线y2=$\frac{6}{x}$相交于A、B两点,且当x>1时,总有y1>y2;当0<x<1时,总有y1<y2;
如图,已知直线y1=x+b与双曲线y2=$\frac{6}{x}$相交于A、B两点,且当x>1时,总有y1>y2;当0<x<1时,总有y1<y2;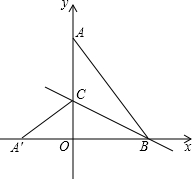 如图,在平面直角坐标系中,点A(0,4),B(3,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,求直线BC的解析式.
如图,在平面直角坐标系中,点A(0,4),B(3,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,求直线BC的解析式.