题目内容
11.已知抛物线y=-x2+bx+c经过点M(2,3),点N(-3,-12).(1)求这个二次函数的解析式;
(2)设抛物线与x轴的负半轴交于A点,与y轴的交点为C点,在抛物线的对称轴上是否存在点Q,使AC=AQ?若存在,求出Q点坐标;若不存在,请说明理由;
(3)将抛物线平移,使抛物线的顶点为E(h,k)(h>0,k>0),设平移后的抛物线与x轴的交点为A1、B(A1在B点的左侧),与y轴的正半轴交点为D,在四边形A1BED中满足${S_{△BED}}=2{S_{△{A_1}OD}}$,且顶点E恰好落在直线y=-2x+2上,求此抛物线的解析式.
分析 (1)将M、N点的坐标代入到抛物线解析式中,得出关于b、c的二元一次方程,解方程即可得出结论;
(2)假设存在,将(1)中得出的抛物线的解析式改写成顶点式,设出点Q的坐标为(1,m),分别令x=0、y=0求出A、C点的坐标,根据两点间的距离公式结合AC=AQ即可得出关于m的无理方程,解方程即可得出结论;
(3)根据(1)的结论结合平移的性质写出平移后的抛物线的解析式,分别令x=0、y=0得出A1、B、D点的坐标,结合顶点在直线y=-2x+2上以及${S_{△BED}}=2{S_{△{A_1}OD}}$,得出关于h、k的方程,解方程即可得出结论.
解答 解:(1)将点M(2,3),点N(-3,-12)代入到抛物线y=-x2+bx+c中,
得$\left\{\begin{array}{l}{3=-4+2b+c}\\{-12=-9-3b+c}\end{array}\right.$,解得:$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$.
∴这个二次函数的解析式为y=-x2+2x+3.
(2)假设存在.
∵二次函数的解析式为y=-x2+2x+3=-(x-1)2+4,
∴设Q点坐标为(1,m).
令y=0,则有-x2+2x+3=0,
解得:x=-1,或x=3,
∴A点的坐标为(-1,0).
令x=0,则y=3,
即点C的坐标为(0,3).
∵AC=$\sqrt{[0-(-1)]^{2}+(3-0)^{2}}$=$\sqrt{10}$,AQ=$\sqrt{[1-(-1)]^{2}+{m}^{2}}$,
∴$\sqrt{10}$=$\sqrt{[1-(-1)]^{2}+{m}^{2}}$,解得:m=±$\sqrt{6}$.
故在抛物线的对称轴上存在点Q,使AC=AQ,Q点坐标为(1,-$\sqrt{6}$)或(1,6).
(3)过点E作EF⊥y轴于点F,如图所示.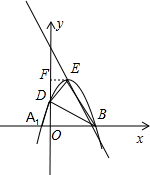
∵平移后抛物线的顶点坐标为E(h,k),
∴平移后的抛物线解析式为y=-(x-h)2+k,点F的坐标为(0,k).
令y=0,则有-(x-h)2+k=0,
解得:x=h-$\sqrt{k}$,或x=h+$\sqrt{k}$,
即点A1的坐标为(h-$\sqrt{k}$,0),点B坐标为(h+$\sqrt{k}$,0).
令x=0,则y=-h2+k,
即点D坐标为(0,k-h2).
${S}_{△{A}_{1}OD}$=$\frac{1}{2}$OA1•OD=$\frac{1}{2}$($\sqrt{k}$-h)(k-h2),${S}_{△BDF}=\frac{1}{2}(EF+OB)•OF$-$\frac{1}{2}$EF•FD-$\frac{1}{2}$OB•OD=$\frac{1}{2}$hk+$\frac{1}{2}$${h}^{2}\sqrt{k}$.
由点E在直线y=-2x+2上,且${S_{△BED}}=2{S_{△{A_1}OD}}$,
可知:$\left\{\begin{array}{l}{k=-2h+2}\\{\frac{1}{2}hk+\frac{1}{2}{h}^{2}\sqrt{k}=(\sqrt{k}-h)(k-{h}^{2})}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=1}\\{h=\frac{1}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{k=10-4\sqrt{6}}\\{h=2\sqrt{6}-4}\end{array}\right.$.
∵k-h2>0,
∴$\left\{\begin{array}{l}{k=10-4\sqrt{6}}\\{h=2\sqrt{6}-4}\end{array}\right.$(舍去).
故平移后抛物线的解析式为y=-$(x-\frac{1}{2})^{2}+1$.
点评 本题考查了待定系数法求函数解析式、两点间的距离公式、解无理方程、三角形的面积公式以及二次函数的性质,解题的关键是:(1)待定系数法求函数解析式;(2)解无理方程;(3)通过分割多边形求三角形的面积.本题属于中档题,(1)(2)难度不大;(3)难度不小,通过分割多边形找出三角形的面积,结合面积间的关系可得出h、k的方程,通过消元得出关于k的一元四次方程,通过分解因式得出k的值,最后再通过点D在y轴正半轴确定k的值,稍显繁琐.

| A. | y=3x+1 | B. | y=ax2+bx+c | C. | y=x2+3 | D. | y=(x-1)2-x2 |
| 甲 | 乙 | 丙 | 丁 | |
| 平均数/环 | 9.7 | 9.5 | 9.5 | 9.7 |
| 方差/环2 | 5.1 | 4.7 | 4.5 | 4.5 |
| A. | -21 | B. | -1 | C. | 9 | D. | 11 |
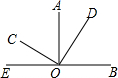 如图,已知AO⊥OB,CO⊥DO,∠BOC=β°,则∠AOD的度数为( )
如图,已知AO⊥OB,CO⊥DO,∠BOC=β°,则∠AOD的度数为( )| A. | β°-90° | B. | 2β°-90° | C. | 180°-β° | D. | 2β°-180° |
| A. | $\left\{\begin{array}{l}{\frac{1}{x}+y=4}\\{x-y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{4x+3y=6}\\{2x+y=4}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=4}\\{x-y=4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{3x+5y=25}\\{x+10y=25}\end{array}\right.$ |
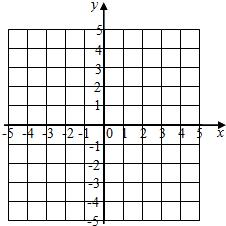 如图,在平面直角坐标系中,分别描出下列各点A(0,0),B(5,4),C(3,0),D(5,1),E(5,-1),F(4,-2),并按A-B-C-D-E-C-F-A顺序连接起来.
如图,在平面直角坐标系中,分别描出下列各点A(0,0),B(5,4),C(3,0),D(5,1),E(5,-1),F(4,-2),并按A-B-C-D-E-C-F-A顺序连接起来.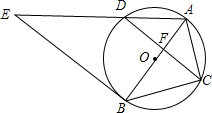 如图,⊙O是△ABC的外接圆,AB经过点O,CD是弦,且CD⊥AB于点F,连接AD,过点B的直线与线段AD的延长线交于点E,且∠E=∠ACF.
如图,⊙O是△ABC的外接圆,AB经过点O,CD是弦,且CD⊥AB于点F,连接AD,过点B的直线与线段AD的延长线交于点E,且∠E=∠ACF.