题目内容
8.求满足“三角形的三边长为整数且三角形的内切圆半径为2”的所有的三角形的三边.分析 设直角三角形的三边长分别为a,b,c,其中c为斜边,于是得到直角三角形内切圆的半径为r=$\frac{a+b-c}{2}$=2,得到a+b=c+4根据勾股定理得到a2+b2=(a+b-4)2,推出$\left\{\begin{array}{l}{a-4=1}\\{b-4=8}\end{array}\right.$或$\left\{\begin{array}{l}{a-4=2}\\{b-4=4}\end{array}\right.$,或$\left\{\begin{array}{l}{a=5}\\{b=12}\end{array}\right.$,或$\left\{\begin{array}{l}{a=6}\\{b=8}\end{array}\right.$,于是得到结论.
解答 解:设直角三角形的三边长分别为a,b,c,其中c为斜边,
∴直角三角形内切圆的半径为r=$\frac{a+b-c}{2}$=2,
∴a+b=c+4,
∵a2+b2=c2,
∴a2+b2=(a+b-4)2,
即ab-4(a+b)+8=0,
∴(a-4)(b-6)=8,
∵三边长为整数,
∴$\left\{\begin{array}{l}{a-4=1}\\{b-4=8}\end{array}\right.$或$\left\{\begin{array}{l}{a-4=2}\\{b-4=4}\end{array}\right.$,或$\left\{\begin{array}{l}{a=5}\\{b=12}\end{array}\right.$,或$\left\{\begin{array}{l}{a=6}\\{b=8}\end{array}\right.$,
①当直角三角形的直角边为5,12时,斜边为13,
②当直角三角形的直角边为6,8时,斜边为10,
综上所述:三角形的三边为:5,12,13或6,8,10.
点评 本题考查了三角形的内切圆与内心,直角三角形的性质,勾股定理,熟练掌握勾股定理是解题的关键.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案| A. | -21 | B. | -1 | C. | 9 | D. | 11 |
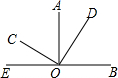 如图,已知AO⊥OB,CO⊥DO,∠BOC=β°,则∠AOD的度数为( )
如图,已知AO⊥OB,CO⊥DO,∠BOC=β°,则∠AOD的度数为( )| A. | β°-90° | B. | 2β°-90° | C. | 180°-β° | D. | 2β°-180° |
 若关于x的不等式x-m>-1的解集如图所示,则m等于( )
若关于x的不等式x-m>-1的解集如图所示,则m等于( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
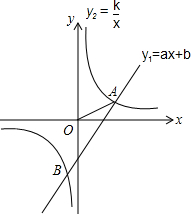 如图.点A(3,1),B(-1,n)是一次函数y1=ax+b和反比例函数y2=$\frac{k}{x}$图象的交点.
如图.点A(3,1),B(-1,n)是一次函数y1=ax+b和反比例函数y2=$\frac{k}{x}$图象的交点.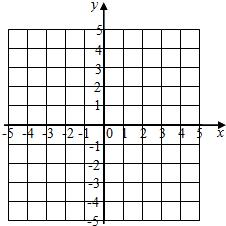 如图,在平面直角坐标系中,分别描出下列各点A(0,0),B(5,4),C(3,0),D(5,1),E(5,-1),F(4,-2),并按A-B-C-D-E-C-F-A顺序连接起来.
如图,在平面直角坐标系中,分别描出下列各点A(0,0),B(5,4),C(3,0),D(5,1),E(5,-1),F(4,-2),并按A-B-C-D-E-C-F-A顺序连接起来.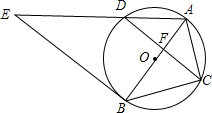 如图,⊙O是△ABC的外接圆,AB经过点O,CD是弦,且CD⊥AB于点F,连接AD,过点B的直线与线段AD的延长线交于点E,且∠E=∠ACF.
如图,⊙O是△ABC的外接圆,AB经过点O,CD是弦,且CD⊥AB于点F,连接AD,过点B的直线与线段AD的延长线交于点E,且∠E=∠ACF. 一只蚂蚁从长为4cm、宽为3cm,高是12cm的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是$\sqrt{193}$.
一只蚂蚁从长为4cm、宽为3cm,高是12cm的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是$\sqrt{193}$.