题目内容
1.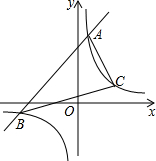 如图,已知直线y1=x+b与双曲线y2=$\frac{6}{x}$相交于A、B两点,且当x>1时,总有y1>y2;当0<x<1时,总有y1<y2;
如图,已知直线y1=x+b与双曲线y2=$\frac{6}{x}$相交于A、B两点,且当x>1时,总有y1>y2;当0<x<1时,总有y1<y2;(1)求b的值及A、B两点的坐标;
(2)若在y2=$\frac{6}{x}$(x>0)上有一点C到y轴的距离为3,求△ABC的面积.
分析 (1)判断出点A的横坐标是1,然后利用反比例函数解析式求出点A的坐标,再代入直线解析式计算即可求出b的值,联立两函数解析式,解方程组即可得到点B的坐标;
(2)根据点C到y轴的距离为3得到点C的坐标,构建矩形利用割补法可求三角形面积.
解答 解:(1)∵当x>1时,y1>y2,当0<x<1时,y1<y2,
∴点A的横坐标为1,
又点A在y2=$\frac{6}{x}$上,
∴点A的坐标为(1,6),
将A(1,6)代入y1=x+b得:b=5,
由y=x+5与y=$\frac{6}{x}$联立解得(1,6)或(-6,-1),
∵点B在第三象限,
∴点B的坐标为(-6,-1);
(2)在y=$\frac{6}{x}$中,当x=3时,y=2,
所以△ABC的面积=7×9-$\frac{1}{2}×$9×3-$\frac{1}{2}$×7×7-$\frac{1}{2}$×2×4=21.
点评 本题考查反比例函数与一次函数的交点,主要利用了待定系数法求一次函数解析式,联立两函数解析式求交点坐标,本题难点在于根据函数值的大小判断出点A、B中有一个点的横坐标是1,从而求出交点坐标,这也是解答本题的突破口.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列函数是二次函数的是( )
| A. | y=3x+1 | B. | y=ax2+bx+c | C. | y=x2+3 | D. | y=(x-1)2-x2 |
6.“掷实心球”是我市初中毕业生体育测试项目之一.测试时,记录下学生掷实心球的成绩,然后按照评分标准转化为相应的分数,满分10分.其中男生掷实心球的评分标准如下:
某校九年级有500名男生参加掷实心球模拟测试,现从中随机抽取10名男生测试成绩(单位:米)如下:
7.39 8.69 9.41 7.50 8.50 7.89 11.11 8.31 6.09 8.11
请完成下列问题:
(1)求这10名男生掷实心球成绩的平均数;
(2)这10名男生掷实心球得分的众数是10,中位数是9;
(3)如果将9分(含9分)以上定为“优秀”,请你估计这500名男生在这次模拟测试中得优秀的人数.
| 成绩(米) | … | 6.00~6.49 | 6.50~6.99 | 7.00~7.49 | 7.50~7.99 | 8.00~8.49 | 8.50及以上 |
| 得分(分) | … | 5 | 6 | 7 | 8 | 9 | 10 |
7.39 8.69 9.41 7.50 8.50 7.89 11.11 8.31 6.09 8.11
请完成下列问题:
(1)求这10名男生掷实心球成绩的平均数;
(2)这10名男生掷实心球得分的众数是10,中位数是9;
(3)如果将9分(含9分)以上定为“优秀”,请你估计这500名男生在这次模拟测试中得优秀的人数.
13.某校射击队从甲、乙、丙、丁四人中选拔一人参加市运会射击比赛.在选拔赛中,每人射击10次,他们10次成绩的平均数及方差如下表所示.
请你根据表中数据选一人参加比赛,最合适的人选是丁.
| 甲 | 乙 | 丙 | 丁 | |
| 平均数/环 | 9.7 | 9.5 | 9.5 | 9.7 |
| 方差/环2 | 5.1 | 4.7 | 4.5 | 4.5 |
10.计算2-1×8-|-5|的结果是( )
| A. | -21 | B. | -1 | C. | 9 | D. | 11 |
20.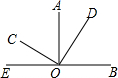 如图,已知AO⊥OB,CO⊥DO,∠BOC=β°,则∠AOD的度数为( )
如图,已知AO⊥OB,CO⊥DO,∠BOC=β°,则∠AOD的度数为( )
 如图,已知AO⊥OB,CO⊥DO,∠BOC=β°,则∠AOD的度数为( )
如图,已知AO⊥OB,CO⊥DO,∠BOC=β°,则∠AOD的度数为( )| A. | β°-90° | B. | 2β°-90° | C. | 180°-β° | D. | 2β°-180° |
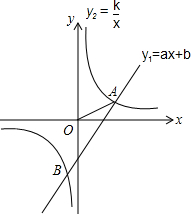 如图.点A(3,1),B(-1,n)是一次函数y1=ax+b和反比例函数y2=$\frac{k}{x}$图象的交点.
如图.点A(3,1),B(-1,n)是一次函数y1=ax+b和反比例函数y2=$\frac{k}{x}$图象的交点.