题目内容
20.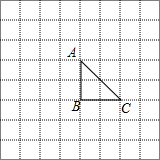 如图,△ABC在网格图中,张晗同学在该网格图中建立直角坐标系,使得B为原点,若S△ACD=2S△ABC,则点D的坐标不可能为( )
如图,△ABC在网格图中,张晗同学在该网格图中建立直角坐标系,使得B为原点,若S△ACD=2S△ABC,则点D的坐标不可能为( )| A. | (-2,2) | B. | (4,2) | C. | (-2,0) | D. | (-4,2) |
分析 可先求得△ABC的面积,则可求得△ACD的面积,再对四个选项分别求△ACD的面积进行判断即可.
解答 解:
由题意可知B(0,0),A(0,2),C(2,0),
∴AB=BC=2,AC=2$\sqrt{2}$,
∴S△ABC=$\frac{1}{2}$×2×2=2,
∴S△ACD=2S△ABC=4,
当D点坐标为(-2,2)时,则AD=2,
∴S△ACD=$\frac{1}{2}$×2×2=2,
当D点坐标为(4,2)时,则AD=4,
∴S△ACD=$\frac{1}{2}$×4×2=4,
当D点坐标为(-2,0)时,则AD=4,
∴S△ACD=$\frac{1}{2}$×4×2=2,
当D点坐标为(-4,2)时,则AD=4,
∴S△ACD=$\frac{1}{2}$×4×2=4,
∴D点坐标不可能是(-2,2),
故选A.
点评 本题主要考查坐标与图形的性质,由所给D点的坐标求得AD的长是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.我市欲从某师范院校招聘一名“特岗教师”,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如表:
根据录用程序,作为人们教师面试的成绩应该比笔试的成绩更重要,并分别赋予它们6和4的权.根据四人各自的平均成绩,你认为将录取( )
| 候选人 | 甲 | 乙 | 丙 | 丁 | |
| 测试成绩 | 面试 | 86 | 91 | 90 | 83 |
| 笔试 | 90 | 83 | 83 | 92 | |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
8. 一列火车A从甲站到乙站,同时另一列火车B从乙站到甲站,如图分别表示它们离甲站的距离与时间的关系,给出以下结论:
一列火车A从甲站到乙站,同时另一列火车B从乙站到甲站,如图分别表示它们离甲站的距离与时间的关系,给出以下结论:
①火车B的速度大于火车A的速度;②行驶1.4小时后,两车相遇;③两车相距110千米时,它们行驶了1个小时;④A车行驶3小时,两车相距300千米,其中正确的结论有( )
 一列火车A从甲站到乙站,同时另一列火车B从乙站到甲站,如图分别表示它们离甲站的距离与时间的关系,给出以下结论:
一列火车A从甲站到乙站,同时另一列火车B从乙站到甲站,如图分别表示它们离甲站的距离与时间的关系,给出以下结论:①火车B的速度大于火车A的速度;②行驶1.4小时后,两车相遇;③两车相距110千米时,它们行驶了1个小时;④A车行驶3小时,两车相距300千米,其中正确的结论有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.在下列各数中,是无理数的是( )
| A. | -$\sqrt{4}$ | |
| B. | π | |
| C. | 3.1415 | |
| D. | 0.1010101…(相邻的两个1之间有1个0) |
5.下列各数不是无理数的是( )
| A. | $\sqrt{7}$ | |
| B. | 0.5 | |
| C. | 0.151151115…(两个5之间依次多一个1) | |
| D. | 2π |
12.y是x的正比例函数,当x=2时,y=4,那么x=-1时,则y等于( )
| A. | 2 | B. | 1 | C. | -2 | D. | -1 |
9.若a>b,则下列不等式一定成立的是( )
| A. | a-b<0 | B. | $\frac{a}{3}$<$\frac{b}{3}$ | C. | 2+2b>2+2a | D. | -a<-b |
 如图,已知∠AOB=90°,如果射线OA、OB同时绕点O逆时针旋转(当射线OA旋转360°后,两条射线同时停止旋转),射线OA以每秒3°的速度旋转至OC,射线OB以每秒1°的速度旋转至OD,当∠COD=60°时,求∠AOD的度数.
如图,已知∠AOB=90°,如果射线OA、OB同时绕点O逆时针旋转(当射线OA旋转360°后,两条射线同时停止旋转),射线OA以每秒3°的速度旋转至OC,射线OB以每秒1°的速度旋转至OD,当∠COD=60°时,求∠AOD的度数.