题目内容
12．y是x的正比例函数，当x=2时，y=4，那么x=-1时，则y等于（ ）| A． | 2 | B． | 1 | C． | -2 | D． | -1 |
分析 先求出正比例函数的解析式，再把x=-1代入求出y的值即可．
解答 解：设正比例函数的解析式为y=kx（k≠0），
∵当x=2时，y=4，
∴2k=4，解得k=2，
∴正比例函数的解析式为y=2x，
∴x=-1时，y=-2．
故选C．
点评 本题考查的是正比例函数的定义，熟知一般地，形如y=kx（k是常数，k≠0）的函数叫做正比例函数是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，把面积为a的正三角形ABC的各边依次循环延长一倍，顺次连接这三条线段的外端点，这样操作后，可以得到一个新的正三角形DEF；对新三角形重复上述过程，经过2016次操作后，所得正三角形的面积是72016a．
3．若a＜b，则下列说法错误的是（ ）
| A． | a+3＜b+3 | B． | 3-2a＞3-2b | C． | a-3＞b-3 | D． | 3b＞3a |
20．
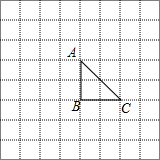如图，△ABC在网格图中，张晗同学在该网格图中建立直角坐标系，使得B为原点，若S△ACD=2S△ABC，则点D的坐标不可能为（ ）
如图，△ABC在网格图中，张晗同学在该网格图中建立直角坐标系，使得B为原点，若S△ACD=2S△ABC，则点D的坐标不可能为（ ）| A． | （-2，2） | B． | （4，2） | C． | （-2，0） | D． | （-4，2） |
7．下列说法中不正确的是（ ）
| A． | 若a＞b，则a-1＞b-1 | B． | 若3a＞3b，则a＞b | ||
| C． | 若a＞b，且c≠0，则ac＞bc | D． | 若a＞b，则7-a＜7-b |
17．下列各组二次根式中，化简后是同类二次根式的一组是（ ）
| A． | $\sqrt{3}$和9 | B． | $\sqrt{24}$和$\sqrt{54}$ | C． | $\sqrt{18}$和$\sqrt{3}$ | D． | $\sqrt{2\frac{1}{2}}$和$\sqrt{5}$ |
4．
如图，边长为1的正方形ABCD绕点A按逆时针方向旋转45°，得到正方形AB′C′D′，正方形ABCD与正方形AB′C′D′叠成一个“风筝”ABCC′D′，那么“风筝”的面积是（ ）
如图，边长为1的正方形ABCD绕点A按逆时针方向旋转45°，得到正方形AB′C′D′，正方形ABCD与正方形AB′C′D′叠成一个“风筝”ABCC′D′，那么“风筝”的面积是（ ）| A． | 2-$\frac{\sqrt{3}}{3}$ | B． | 3-$\sqrt{2}$ | C． | $\sqrt{3}$ | D． | $\frac{7}{4}$ |
1．使式子$\sqrt{3-x}$有意义的x的取值范围是（ ）
| A． | x＞3 | B． | x≥3 | C． | x＜3 | D． | x≤3 |
2．多项式3x3-2x2-15的次数为（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 5 |