Question

19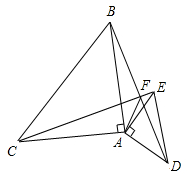．等腰直角△ABC与等腰直角△ADE中，AB=AC，AD=AE，∠BAC=90°，∠DAE=90°，如图，将△ADE绕点A旋转一定度数，连BD、EC，BD与EC交于点F，连AF．求证：
（1）EC⊥BD；
（2）AF平分∠BFE．

Answer 1

分析 （1）根据SAS即可求得△CAE≌△BAD，求得∠ACF=∠ABD．因为∠ANC=∠BNF，根据三角形的内角和定理就可求得∠BFN=∠NAC=90°，从而证得BD⊥CE；
（2）作AG⊥CE于G，AK⊥BD于K．根据三角形面积公式即可求得AG=AK．根据角的平分线的性质定理的逆定理即可证得FA是∠CFD的平分线．

解答 解：（1）记BD与AC交点为N，
∵∠BAC=∠DAE=90°，∠BAE=∠BAE，
∴∠CAE=∠BAD．
在△CAE和△BAD中，
$\left\{\begin{array}{l}{AC=AB}\\{∠CAE=∠BAD}\\{AE=AD}\end{array}\right.$，
∴△CAE≌△BAD（SAS），
∴∠ACF=∠ABD．
∵∠ANC=∠BNF，
∴∠BFN=∠NAC=90°．
∴BD⊥CE．
（2）如图1，作AG⊥CE于G，AK⊥BD于K．

由（1）知△CAE≌△BAD，
∴CE=BD，S_△CAE=S_△BAD，
∴AG=AK．
∴点A在∠CFD的平分线上．       
即 FA是∠CFD的平分线．

点评 本题考查了等腰直角三角形的性质，全等三角形的判定，角的平分线的判定等知识点，利用全等三角形得出线段相等和角相等是解题的关键．