题目内容
4.小明在爬一小山时,第一阶段的平均速度为v,所用的时间为t1,第二阶段的平均速度为$\frac{1}{3}$v,所用时间为t2.下山时,小明的平均速度保持为3v,已知小明上山和下山的路是相同的,那么小明下山用了多长时间?$\frac{1}{3}{t}_{1}+\frac{{t}_{2}}{9}$.分析 根据题意可以得到小明上山的路程,由小明上山和下山的路是相同的,下山时,小明的平均速度保持为3v,从而可以求得小明下上用的时间.
解答 解:由题意可得,
小明下山用的时间是:$\frac{v{t}_{1}+\frac{v}{3}{t}_{2}}{3v}=\frac{{t}_{1}}{3}+\frac{{t}_{2}}{9}$,
故答案为:$\frac{1}{3}{t}_{1}+\frac{{t}_{2}}{9}$.
点评 本题考查列代数式,解题的关键是明确题意,列出相应的代数式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.已知⊙O的面积为3π,则其内接正三角形的面积为( )
| A. | 9$\sqrt{3}$ | B. | $\frac{9\sqrt{3}}{4}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | $\frac{9\sqrt{6}}{4}$ |
13.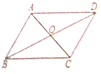 如图,在平行四边形ABCD中,已知AC、BD相交于点O,两条对角线的和为20cm,CD的长为4cm,则△OAB的周长是( )
如图,在平行四边形ABCD中,已知AC、BD相交于点O,两条对角线的和为20cm,CD的长为4cm,则△OAB的周长是( )
 如图,在平行四边形ABCD中,已知AC、BD相交于点O,两条对角线的和为20cm,CD的长为4cm,则△OAB的周长是( )
如图,在平行四边形ABCD中,已知AC、BD相交于点O,两条对角线的和为20cm,CD的长为4cm,则△OAB的周长是( )| A. | 10cm | B. | 8cm | C. | 14cm | D. | 12cm |
18.若|m-n-3|+(m+n+1)2=0,则m+2n的值为( )
| A. | -1 | B. | -3 | C. | 0 | D. | 3 |
 为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时,为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制成两幅不完整的统计图如图所示,则抽查的学生中户外活动时间为1.5小时的人数12.
为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时,为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制成两幅不完整的统计图如图所示,则抽查的学生中户外活动时间为1.5小时的人数12. 在某次学校安全知识抢答赛中,九年级参赛的10名学生的成绩统计图如图所示.这10名学生的参赛成绩的中位数是90分.
在某次学校安全知识抢答赛中,九年级参赛的10名学生的成绩统计图如图所示.这10名学生的参赛成绩的中位数是90分.
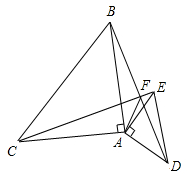 等腰直角△ABC与等腰直角△ADE中,AB=AC,AD=AE,∠BAC=90°,∠DAE=90°,如图,将△ADE绕点A旋转一定度数,连BD、EC,BD与EC交于点F,连AF.求证:
等腰直角△ABC与等腰直角△ADE中,AB=AC,AD=AE,∠BAC=90°,∠DAE=90°,如图,将△ADE绕点A旋转一定度数,连BD、EC,BD与EC交于点F,连AF.求证: