题目内容
6.我们知道两直线交于一点,对顶角有2对,三条直线交于一点,对顶角有6对,四条直线交于一点,对顶角有12对,…(1)10条直线交于一点,对顶角有90对.
(2)n(n≥2)条直线交于一点,对顶角有n(n-1)对.
分析 (1)仔细观察计算对顶角的式子,发现式子不变的部分及变的部分的规律,求出本题结论;
(2)利用(1)中规律得出答案即可.
解答  解:(1)如图①两条直线交于一点,图中共有$\frac{(4-2)×4}{4}$=2对对顶角;如图②三条直线交于一点,图中共有$\frac{(6-2)×6}{4}$=6对对顶角;如图③四条直线交于一点,图中共有$\frac{(8-2)×8}{4}$=12对对顶角;
解:(1)如图①两条直线交于一点,图中共有$\frac{(4-2)×4}{4}$=2对对顶角;如图②三条直线交于一点,图中共有$\frac{(6-2)×6}{4}$=6对对顶角;如图③四条直线交于一点,图中共有$\frac{(8-2)×8}{4}$=12对对顶角;
…;
按这样的规律,10条直线交于一点,那么对顶角共有:$\frac{(20-2)×20}{4}$=90,
故答案为:90;
(2)由(1)得:n(n≥2)条直线交于一点,对顶角有:$\frac{2n(2n-2)}{4}$=n(n-1).
故答案为:n(n-1).
点评 此题主要考查了对顶角以及图形变化规律,本题是一个探索规律型的题目,解决时注意观察每对数之间的关系.这是中考中经常出现的问题.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
11.(-3)2的结果是( )
| A. | 6 | B. | -6 | C. | 9 | D. | -9 |
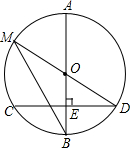 如图,AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,点M在⊙O上,MD经过圆心O,联结MB.
如图,AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,点M在⊙O上,MD经过圆心O,联结MB. 4个大小相同的正方体积木摆放成如图所示的几何体,其俯视图是( )
4个大小相同的正方体积木摆放成如图所示的几何体,其俯视图是( )



 在平面直角坐标系中,一个二次函数的图象经过A(1,0)、B(3,0)两点.
在平面直角坐标系中,一个二次函数的图象经过A(1,0)、B(3,0)两点. 如图,已知函数y1=2x-1和y2=x-3的图象交于点P(-2,-5),则根据图象可得不等式y1>y2的解集是x>-2.
如图,已知函数y1=2x-1和y2=x-3的图象交于点P(-2,-5),则根据图象可得不等式y1>y2的解集是x>-2. 如图,在矩形ABCD中,AB=2$\sqrt{3}$,BC=6,将该矩形沿对角线BD翻折,C的对应点为G,使△DBG与△DBC在同一平面内,BG交AD于点E,在DA延长线上取点F,使AE=AF,连接BF.
如图,在矩形ABCD中,AB=2$\sqrt{3}$,BC=6,将该矩形沿对角线BD翻折,C的对应点为G,使△DBG与△DBC在同一平面内,BG交AD于点E,在DA延长线上取点F,使AE=AF,连接BF.