题目内容
12.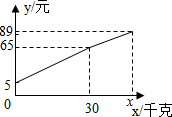 一位农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用.他将土豆按市场价售出一些后,又降价出售.售出土豆的质量x(千克)与他手中持有的钱数y(元)(含备用零钱)的函数关系如图所示.结合图象回答下列问题:
一位农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用.他将土豆按市场价售出一些后,又降价出售.售出土豆的质量x(千克)与他手中持有的钱数y(元)(含备用零钱)的函数关系如图所示.结合图象回答下列问题:(1)农民自带的零钱是多少元?
(2)土豆的市场价为多少元?
(3)降价后他按每千克1.6元将剩余土豆售完,这时他手中的钱(含备用零钱)是89元,问他一共带了多少千克土豆?
分析 (1)由图象可知,当x=0时,y=5,所以农民自带的零钱是5元.
(2)可设降价前每千克土豆价格为k元,则可列出农民手中钱y与所售土豆千克数x之间的函数关系式,由图象知,当x=30时,y的值,从而求出这个函数式.
(3)可设降价后农民手中钱y与所售土豆千克数x之间的函数关系式,因为当x=a时,y=89,当x=30时,y=65,依此列出方程求解.
解答 解:(1)由图象可知,当x=0时,y=5.
答:农民自带的零钱是5元.
(2)设降价前每千克土豆价格为k元,
则农民手中钱y与所售土豆千克数x之间的函数关系式为:y=kx+5,
∵当x=30时,y=65,
∴65=30k+5,
解得k=2.
答:降价前每千克土豆价格为2元.
(3)设降价后农民手中钱y与所售土豆千克数x之间的函数关系式为y=1.6x+b.
∵当x=30时,y=65,
即1.6×30+b=65
∴b=17,
当x=a时,y=89,即1.6a+17=89,
解得:a=45.
答:农民一共带了45千克土豆
点评 此题考查了一次函数的实际应用问题.此题难度适中,解题的关键是仔细分析函数图象,从中找寻信息,利用待定系数法求出函数解析式,从而解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.某商场计划购进两种服装共100件,这两种服装的进价、售价如表所示:
(1)若商场预计进货用3500元,则这两种服装个购进多少件?
(2)若商场规定B种服装进货数量不超过A种服装进货数量的三倍,且超过A种服装进货数量的2倍,求商场有几种进货方案;
(3)在(2)条件下应该怎样进货才能使商场销售完这批货时获利最多?此时利润为多少元?
| 价格 类型 | 进价(元/件) | 售价(元/件) |
| A | 30 | 45 |
| 售价(元/部) | 50 | 70 |
(2)若商场规定B种服装进货数量不超过A种服装进货数量的三倍,且超过A种服装进货数量的2倍,求商场有几种进货方案;
(3)在(2)条件下应该怎样进货才能使商场销售完这批货时获利最多?此时利润为多少元?
 如图,已知在正方形ABCD中,AE=EB,AF=$\frac{1}{4}$AD,求证:CE⊥EF.
如图,已知在正方形ABCD中,AE=EB,AF=$\frac{1}{4}$AD,求证:CE⊥EF.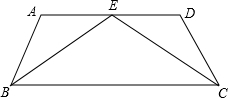 如图,AD∥BC,∠A=94°,∠D=106°,BE、CE分别是∠ABC和∠BCD的角平分线,求∠BEC的度数.
如图,AD∥BC,∠A=94°,∠D=106°,BE、CE分别是∠ABC和∠BCD的角平分线,求∠BEC的度数.
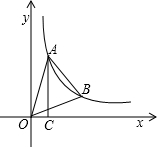 如图,点A、B在反比例函数y=$\frac{k}{x}$的图象上,且点A、B的横坐标分别为a,2a (a>0).过点A作AC⊥x轴,垂足为C,且△AOC的面积为2.
如图,点A、B在反比例函数y=$\frac{k}{x}$的图象上,且点A、B的横坐标分别为a,2a (a>0).过点A作AC⊥x轴,垂足为C,且△AOC的面积为2.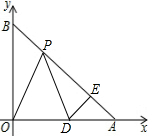 已知在平面直角坐标系中,A(a、o)、B(o、b)满足$\sqrt{a-b}$+|a-3$\sqrt{2}$|=0,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
已知在平面直角坐标系中,A(a、o)、B(o、b)满足$\sqrt{a-b}$+|a-3$\sqrt{2}$|=0,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.