题目内容
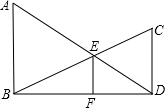如图，AB⊥BD，CD⊥BD，垂足分别为B，D，AD和BC相交于点E，EF⊥BD于F，证明：| 1 |
| AB |
| 1 |
| CD |
| 1 |
| EF |
考点：相似三角形的判定与性质
专题：证明题
分析：易证EF∥AB∥CD，则△ABD∽△EFD，根据相似三角形的对应边的比相等，即可证得
=
，同理，
=
，两式相加即可证得．
| EF |
| AB |
| DF |
| BD |
| EF |
| CD |
| BF |
| BD |
解答：证明：∵AB⊥BD，EF⊥BD，
∴EF∥AB，
∴△ABD∽△EFD，
∴
=
，
同理，
=
，
∴
+
=
=
=1，即（
+
）•EF=1，
∴
+
=
．
∴EF∥AB，
∴△ABD∽△EFD，
∴
| EF |
| AB |
| DF |
| BD |
同理，
| EF |
| CD |
| BF |
| BD |
∴
| EF |
| AB |
| EF |
| CD |
| DF+BF |
| BD |
| BD |
| BD |
| 1 |
| AB |
| 1 |
| CD |
∴
| 1 |
| AB |
| 1 |
| CD |
| 1 |
| EF |
点评：本题考查了相似三角形的判定与性质，正确通过相似三角形的性质把线段的比进行转化是关键．
练习册系列答案
相关题目
已知二次函数y=ax2+bx+c中，其函数y与自变量x之间的部分对应值如下表所示：
点A（x1，y1）、B（x2，y2）在函数的图象上，则当0＜x1＜1，2＜x2＜3时，y1与y2的大小关系正确的是（ ）
| x | … | 0 | 1 | 2 | 3 | … |
| y | … | 5 | 2 | 1 | 2 | … |
| A、y1＜y2 |
| B、y1＞y2 |
| C、y1≥y2 |
| D、y1≤y2 |
已知：△ABC内接正△DEF，AD=BF=CE，求证：△ABC为正三角形．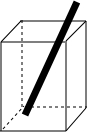
如图，将一根长为20cm的玻璃棒放入一个长为4cm，宽为3cm，高为12cm的长方形容器中，你知道玻璃棒露在外面的部分的长度d在什么范围之内吗？请通过计算写出d的范围．
如图，已知∠ABC与∠ACB的外角∠ACB的平争线交于点D，
如图，CD是Rt△ABC的斜边AB上的高，∠BAC的平分线分别交BC，CD于点E，F．
如图，在平面直角坐标系中，四边形ABCD是正方形，请计算该正方形的面积．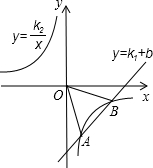
如图，已知一次函数y=k1x+b的图象与反比例函数y=