题目内容
 如图,已知∠ABC与∠ACB的外角∠ACB的平争线交于点D,
如图,已知∠ABC与∠ACB的外角∠ACB的平争线交于点D,(1)若∠A=50°,求∠D的度数;
(2)猜想∠D与∠A的关系,并说明理由.
考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)利用三角形外角的性质和角平分线的性质得到∠2+
∠A=∠1.则∠2-∠1=25°.然后又由三角形外角性质推知∠D=∠2-∠1=25°;
(2)根据(1)的结果可得出结论.
| 1 |
| 2 |
(2)根据(1)的结果可得出结论.
解答:解:(1)∵∠ABC+∠A=∠ACE,∠ABC的平分线和∠ACB的外角平分线交于D,
∴
(∠ABC+∠A)=
∠ACE,即∠2+
∠A=∠1.
又∵∠A=50°,
∴∠2+25°=∠1,
∴∠2-∠1=25°
又∵∠2+∠D=∠1,
∴∠D=∠2-∠1=25°
(2)猜想:∠D=
∠A.
理由:假设∠A=α,
∵∠ABC+∠A=∠ACE,∠ABC的平分线和∠ACB的外角平分线交于D,
∴
(∠ABC+∠A)=
∠ACE,即∠2+
∠A=∠1.
又∵∠A=α,
∴∠2+
α=∠1,
∴∠2-∠1=
α°
又∵∠2+∠D=∠1,
∴∠D=∠2-∠1=
∠A.
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠A=50°,
∴∠2+25°=∠1,
∴∠2-∠1=25°
又∵∠2+∠D=∠1,
∴∠D=∠2-∠1=25°
(2)猜想:∠D=
| 1 |
| 2 |
理由:假设∠A=α,
∵∠ABC+∠A=∠ACE,∠ABC的平分线和∠ACB的外角平分线交于D,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠A=α,
∴∠2+
| 1 |
| 2 |
∴∠2-∠1=
| 1 |
| 2 |
又∵∠2+∠D=∠1,
∴∠D=∠2-∠1=
| 1 |
| 2 |
点评:本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
代数式a-2与1-2a的值相等,则a等于( )
| A、0 | B、1 | C、2 | D、3 |
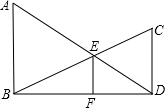 如图,AB⊥BD,CD⊥BD,垂足分别为B,D,AD和BC相交于点E,EF⊥BD于F,证明:
如图,AB⊥BD,CD⊥BD,垂足分别为B,D,AD和BC相交于点E,EF⊥BD于F,证明: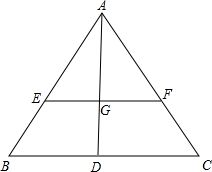 已知AD是△ABC的边BC上的中线,G是三角形的重心,EF过点G且平行于BC,分别交AB、AC于点E、F.求AF:FC和EF:BC的值.
已知AD是△ABC的边BC上的中线,G是三角形的重心,EF过点G且平行于BC,分别交AB、AC于点E、F.求AF:FC和EF:BC的值. 通过对苏科版九(上)教材一道习题的探索研究,“在一次聚会中,有45个人,每两个参加聚会的人都互相握了一次手,一共握了多少次手?”
通过对苏科版九(上)教材一道习题的探索研究,“在一次聚会中,有45个人,每两个参加聚会的人都互相握了一次手,一共握了多少次手?”