题目内容
如图，CD是Rt△ABC的斜边AB上的高，∠BAC的平分线分别交BC，CD于点E，F．（1）求证：CF=CE；
（2）求证：
| CE |
| BE |
| AC |
| AB |
考点：相似三角形的判定与性质
专题：证明题
分析：（1）过点E作EG⊥AB，垂足为G，则CD∥EG，EG=EC，可证得△AEC≌△AEG，所以有∠CEF=∠GEF=∠CFE，所以CF=CE；
（2）由（1）∠GEF=∠CFE可得∠AEB=∠AFC，且∠CAF=∠BAE，所以△ACF∽△ABE，所以
=
．
（2）由（1）∠GEF=∠CFE可得∠AEB=∠AFC，且∠CAF=∠BAE，所以△ACF∽△ABE，所以
| CE |
| BE |
| AC |
| AB |
解答：证明：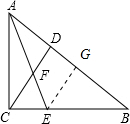
（1）过点E作EG⊥AB，垂足为G，
则CD∥EG，所以∠CFE=∠GEF
且AE为∠BAC的平分线，
所以EC=EG，
所以△AEC≌△AEG，
所以∠CEF=∠GEF，
所以∠CEF=∠CFE，
所以CF=CE；
（2）由（1）知∠CFE=∠CEF，
所以∠AEB=∠AFC，
且∠CAF=∠BAE，
所以△ACF∽△ABE，
所以
=
．
（1）过点E作EG⊥AB，垂足为G，
则CD∥EG，所以∠CFE=∠GEF
且AE为∠BAC的平分线，
所以EC=EG，
所以△AEC≌△AEG，
所以∠CEF=∠GEF，
所以∠CEF=∠CFE，
所以CF=CE；
（2）由（1）知∠CFE=∠CEF，
所以∠AEB=∠AFC，
且∠CAF=∠BAE，
所以△ACF∽△ABE，
所以
| CE |
| BE |
| AC |
| AB |
点评：本题主要考查三角形相似的判断和性质，注意角平分线这个条件的运用，角平分线上的点到角两边的距离相等．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图1，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”（a），中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”（h）．我们可得出一种计算三角形面积的新方法：S△ABC=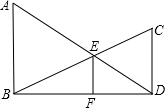
如图，AB⊥BD，CD⊥BD，垂足分别为B，D，AD和BC相交于点E，EF⊥BD于F，证明：
在△ABC中，tanA=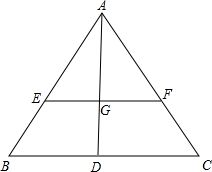
已知AD是△ABC的边BC上的中线，G是三角形的重心，EF过点G且平行于BC，分别交AB、AC于点E、F．求AF：FC和EF：BC的值．
在四边形ABCD，AC与BD相交于点E，AC⊥AB，BD⊥CD，S△EBC=16，S△AED=8．求：