题目内容
 如图,在平面直角坐标系中,四边形ABCD是正方形,请计算该正方形的面积.
如图,在平面直角坐标系中,四边形ABCD是正方形,请计算该正方形的面积.考点:坐标与图形性质,三角形的面积
专题:计算题
分析:先利用正方形的两顶点坐标(-3,0)、(0,4)和勾股定理计算出正方形的边长,然后根据正方形的面积公式求解.
解答: 解:如图,
解:如图,
∵A点坐标为(-3,0),B点坐标为(0,4),
∴OA=3,OB=4,
在Rt△OAB中,AB=
=5,
∴正方形的面积=52=25.
 解:如图,
解:如图,∵A点坐标为(-3,0),B点坐标为(0,4),
∴OA=3,OB=4,
在Rt△OAB中,AB=
| OA2+OB2 |
∴正方形的面积=52=25.
点评:本题考查了坐标与图形性质:利用点的坐标特征计算相应的线段长和判断线段与坐标轴的位置关系;记住各象限内点的坐标特征和坐标上点的坐标特征.

练习册系列答案
相关题目
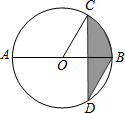 如图AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=4
如图AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=4| 3 |
A、
| ||
B、
| ||
| C、4π | ||
| D、8π |
 如图,天平两边盘中标有相同字母的物体的质量相同,若两架天平保持平衡,则1个砝码A与n个砝码C的质量相等,n的值为( )
如图,天平两边盘中标有相同字母的物体的质量相同,若两架天平保持平衡,则1个砝码A与n个砝码C的质量相等,n的值为( )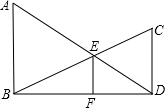 如图,AB⊥BD,CD⊥BD,垂足分别为B,D,AD和BC相交于点E,EF⊥BD于F,证明:
如图,AB⊥BD,CD⊥BD,垂足分别为B,D,AD和BC相交于点E,EF⊥BD于F,证明: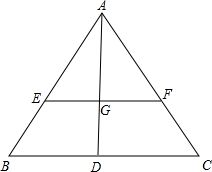 已知AD是△ABC的边BC上的中线,G是三角形的重心,EF过点G且平行于BC,分别交AB、AC于点E、F.求AF:FC和EF:BC的值.
已知AD是△ABC的边BC上的中线,G是三角形的重心,EF过点G且平行于BC,分别交AB、AC于点E、F.求AF:FC和EF:BC的值.
 通过对苏科版九(上)教材一道习题的探索研究,“在一次聚会中,有45个人,每两个参加聚会的人都互相握了一次手,一共握了多少次手?”
通过对苏科版九(上)教材一道习题的探索研究,“在一次聚会中,有45个人,每两个参加聚会的人都互相握了一次手,一共握了多少次手?” 在四边形ABCD,AC与BD相交于点E,AC⊥AB,BD⊥CD,S△EBC=16,S△AED=8.求:
在四边形ABCD,AC与BD相交于点E,AC⊥AB,BD⊥CD,S△EBC=16,S△AED=8.求: