题目内容
已知二次函数y=ax2+bx+c中,其函数y与自变量x之间的部分对应值如下表所示:
点A(x1,y1)、B(x2,y2)在函数的图象上,则当0<x1<1,2<x2<3时,y1与y2的大小关系正确的是( )
| x | … | 0 | 1 | 2 | 3 | … |
| y | … | 5 | 2 | 1 | 2 | … |
| A、y1<y2 |
| B、y1>y2 |
| C、y1≥y2 |
| D、y1≤y2 |
考点:二次函数图象上点的坐标特征
专题:
分析:从图表中得到:对称轴是x=2.当x<2时,y随x的增大而减小.当x>2时,y随x的增大而增大.据此作出判断.
解答:解:根据图表知,
当x=1和x=3时,所对应的y值都是2,∴抛物线的对称轴是直线x=2,
又∵当x>2时,y随x的增大而增大;当x<2时,y随x的增大而减小,
∴该二次函数的图象的开口方向是向上;
∵0<x1<1,2<x2<3,
0<x1<1关于对称轴的对称点在3和4之间,
当x>2时,y随x的增大而增大,
∴y1>y2,
故选:B.
当x=1和x=3时,所对应的y值都是2,∴抛物线的对称轴是直线x=2,
又∵当x>2时,y随x的增大而增大;当x<2时,y随x的增大而减小,
∴该二次函数的图象的开口方向是向上;
∵0<x1<1,2<x2<3,
0<x1<1关于对称轴的对称点在3和4之间,
当x>2时,y随x的增大而增大,
∴y1>y2,
故选:B.
点评:本题主要考查对二次函数图象上点的坐标特征,能根据二次函数的对称性判断两点的纵坐标的大小是解此题的关键.

练习册系列答案
相关题目
要使代数式7-3x的值小于-2,则x的取值范围是( )
| A、x>3 | ||
| B、x<3 | ||
| C、x>-3 | ||
D、x>
|
代数式a-2与1-2a的值相等,则a等于( )
| A、0 | B、1 | C、2 | D、3 |
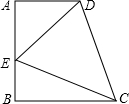 在直角梯形ABCD中,AD∥BC,(AD<BC),AB⊥BC,AB=BC=12,点E在AB边上,连接CE,DE,若∠DCE=45°,DE=10,则线段BE的长为
在直角梯形ABCD中,AD∥BC,(AD<BC),AB⊥BC,AB=BC=12,点E在AB边上,连接CE,DE,若∠DCE=45°,DE=10,则线段BE的长为 如图,天平两边盘中标有相同字母的物体的质量相同,若两架天平保持平衡,则1个砝码A与n个砝码C的质量相等,n的值为( )
如图,天平两边盘中标有相同字母的物体的质量相同,若两架天平保持平衡,则1个砝码A与n个砝码C的质量相等,n的值为( ) 如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=
如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=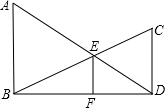 如图,AB⊥BD,CD⊥BD,垂足分别为B,D,AD和BC相交于点E,EF⊥BD于F,证明:
如图,AB⊥BD,CD⊥BD,垂足分别为B,D,AD和BC相交于点E,EF⊥BD于F,证明: 在四边形ABCD,AC与BD相交于点E,AC⊥AB,BD⊥CD,S△EBC=16,S△AED=8.求:
在四边形ABCD,AC与BD相交于点E,AC⊥AB,BD⊥CD,S△EBC=16,S△AED=8.求: