题目内容
18.有甲、乙两个箱子,其中甲箱内有98颗球,分别标记号码1~98,且号码为不重复的整数,乙箱内没有球.已知紫悦从甲箱内拿出m颗球放入乙箱后,乙箱内球的号码的中位数为40,若此时甲箱内剩有a颗球的号码小于40,b颗球的号码大于40.(1)当m=49时,求a、b之值,并问甲箱内球的号码的中位数能否为40?说明理由;
(2)当甲箱内球的号码的中位数与乙箱内球的号码的中位数都是x,求x的值.
分析 (1)根据乙箱内球的号码的中位数确定小于、大于40各有多少,求a、b的值,根据40号球在乙箱内,甲箱内有49颗球,不可能有40号球判断甲箱内球的号码的中位数能否为40;
(2)设在甲箱内球的号码小于x的数量和在乙箱内球的号码小于x数量,列式计算即可.
解答 解:(1)甲箱98-49=49(颗),
∵乙箱中位数40,
∴小于、大于40各有(49-1)÷2=24(颗),
∴甲箱中小于40的球有a=39-24=15(颗),
大于40的有b=49-15=34(颗),
甲箱内球的号码的中位数不能为40,
∵a≠b,(40号球在乙箱内,甲箱内有49颗球,不可能有40号球)
∴甲箱内球的号码的中位数不能为40. (5分)
(2)由(1)可知:当甲、乙箱内球的号码的中位数相同时,甲、乙箱内球的数量应该都是偶数.设在甲箱内球的号码小于x的数量是c颗,则大于x的数量也是c颗;设在乙箱内球的号码小于x数量是d颗,则大于x数量也是d颗,于是在全部98颗球中,号码小于x数量是(c+d)颗,大于x数量也是(c+d)颗,即1~98的中位数是x.
∴x=$\frac{1}{2}$(49+50)=49.5.
点评 本题的是中位数的知识,掌握中位数的概念:中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数)是解题的关键.

练习册系列答案
相关题目
8.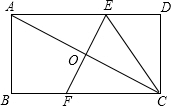 如图,在矩形ABCD中,AB=2,BC=4,将矩形沿EF折叠,使点A与点C重合,连接CE,则CE长为( )
如图,在矩形ABCD中,AB=2,BC=4,将矩形沿EF折叠,使点A与点C重合,连接CE,则CE长为( )
 如图,在矩形ABCD中,AB=2,BC=4,将矩形沿EF折叠,使点A与点C重合,连接CE,则CE长为( )
如图,在矩形ABCD中,AB=2,BC=4,将矩形沿EF折叠,使点A与点C重合,连接CE,则CE长为( )| A. | 3.5 | B. | 3 | C. | 2.8 | D. | 2.5 |
6. 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x>k1x+b的解集为( )
直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x>k1x+b的解集为( )
 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x>k1x+b的解集为( )
直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x>k1x+b的解集为( )| A. | x>3 | B. | x<3 | C. | x>-1 | D. | x<-1 |
10.己知-2xn-3my3与3x7ym+n是同类项,则mn的值是( )
| A. | 4 | B. | 1 | C. | -4 | D. | -1 |
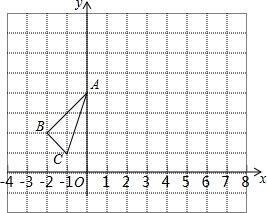 △ABC在平面直角坐标系中的位置如图所示,点O为坐标原点:
△ABC在平面直角坐标系中的位置如图所示,点O为坐标原点: 如图,OC⊥AB于点O,OD平分∠BOC,求∠COD的度数.
如图,OC⊥AB于点O,OD平分∠BOC,求∠COD的度数.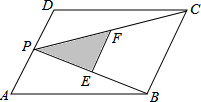 如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1,S2.若S=3,则S1+S2的值为( )
如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1,S2.若S=3,则S1+S2的值为( )